Inquiries-Week 3: Reflect and Rotate
Introduction
Explore the reflection and rotation of polygons to discover the patterns that emerge.
Polygon Play
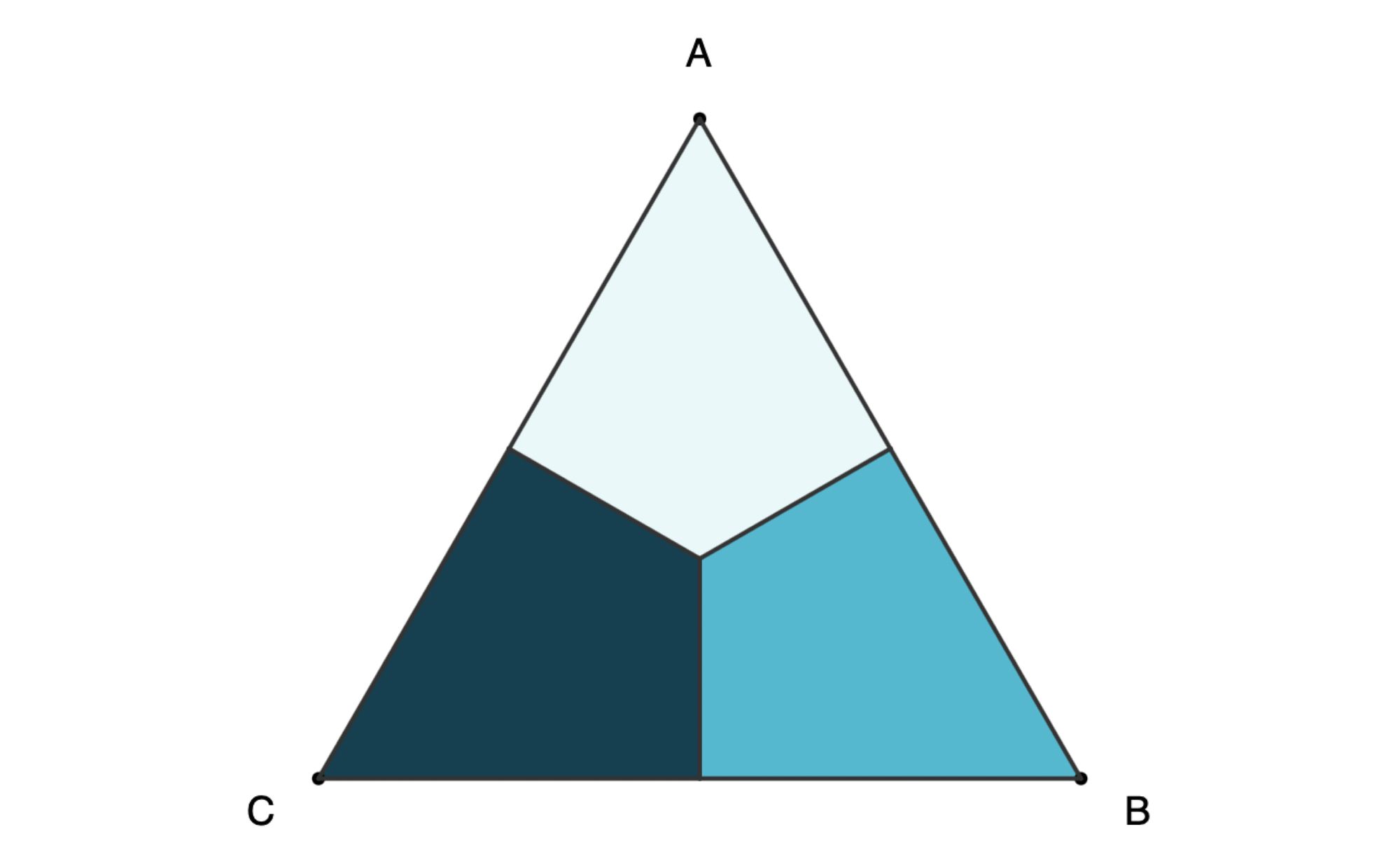
Let's start with a triangle ABC. We can rotate clockwise so that each vertex moves clockwise by one step:
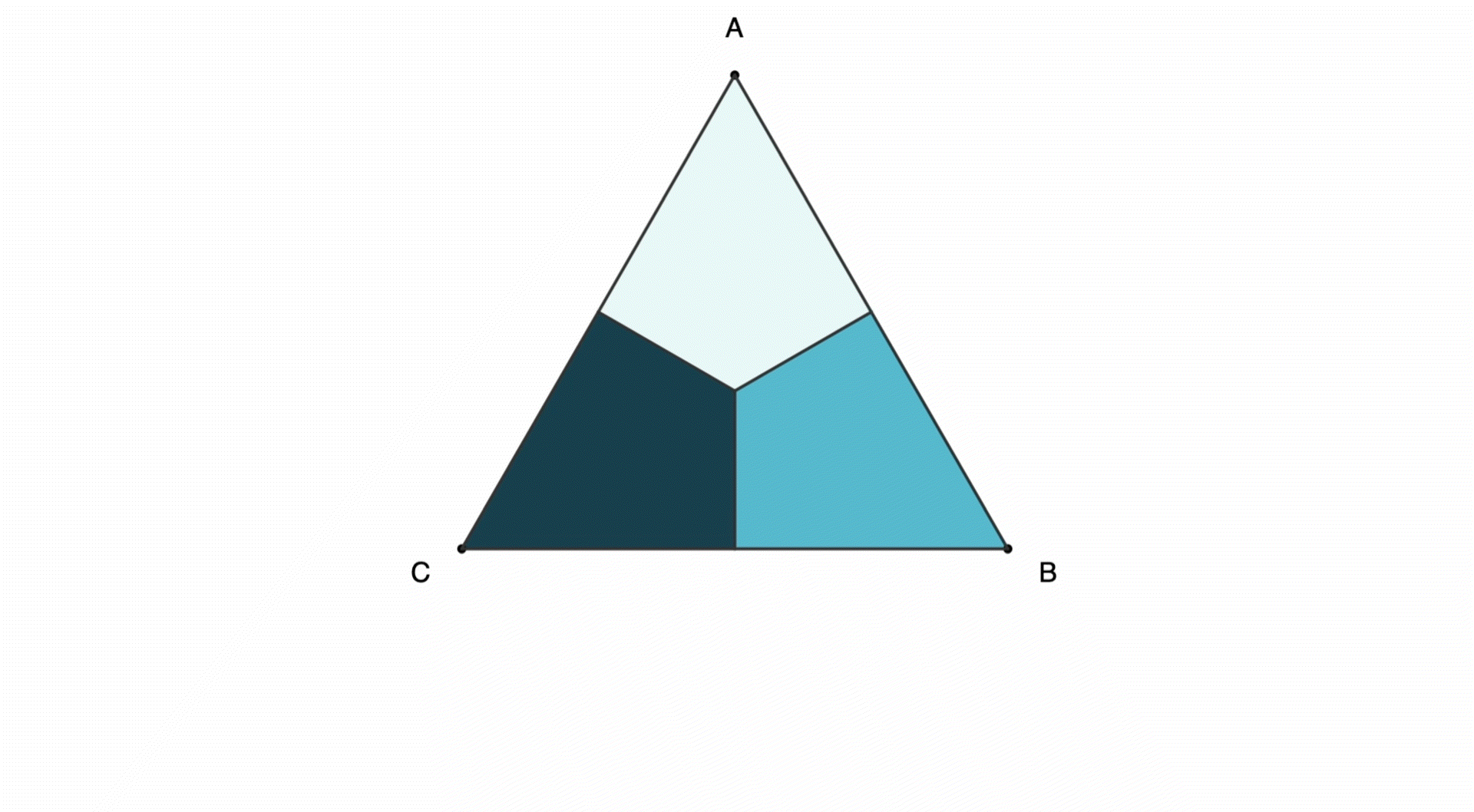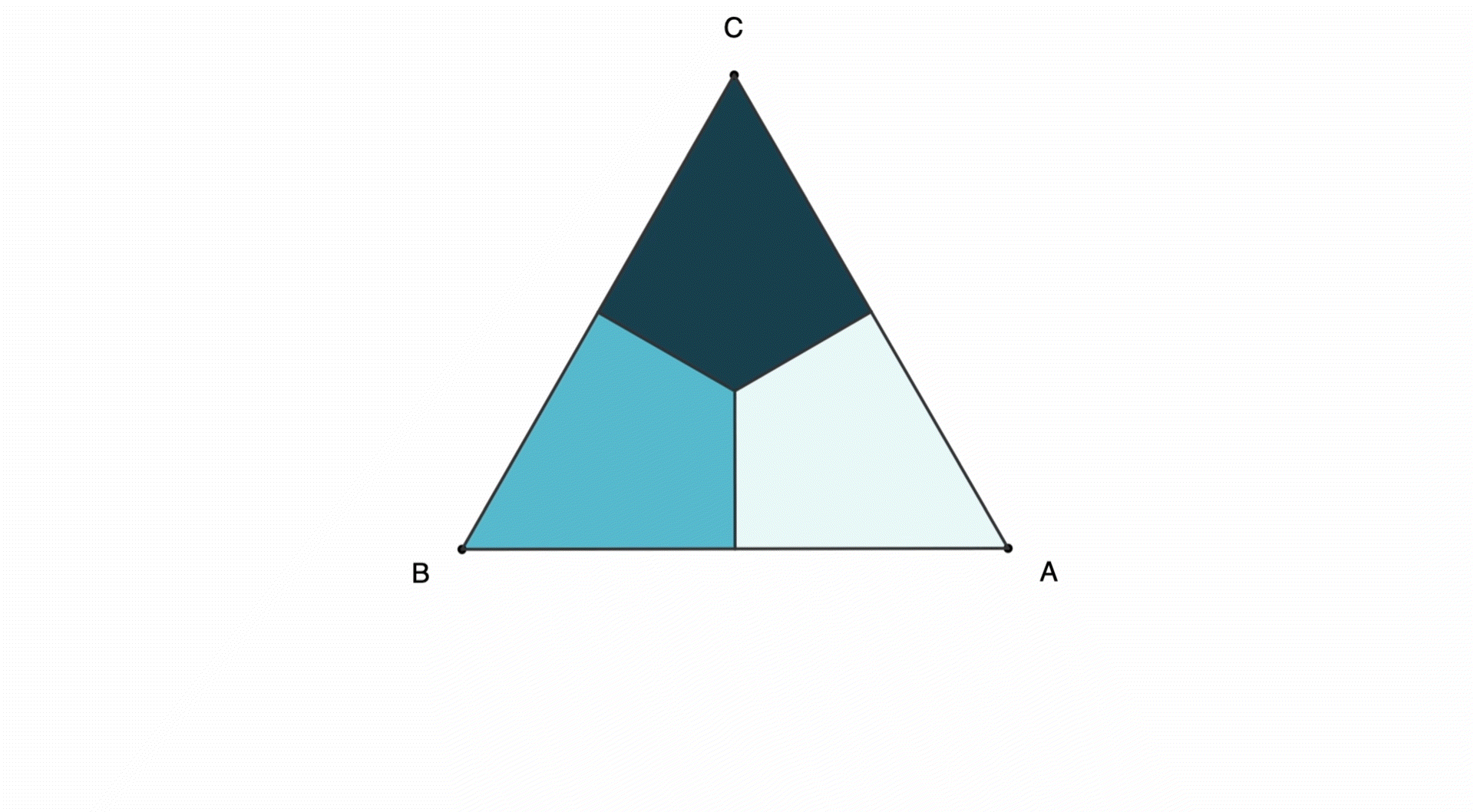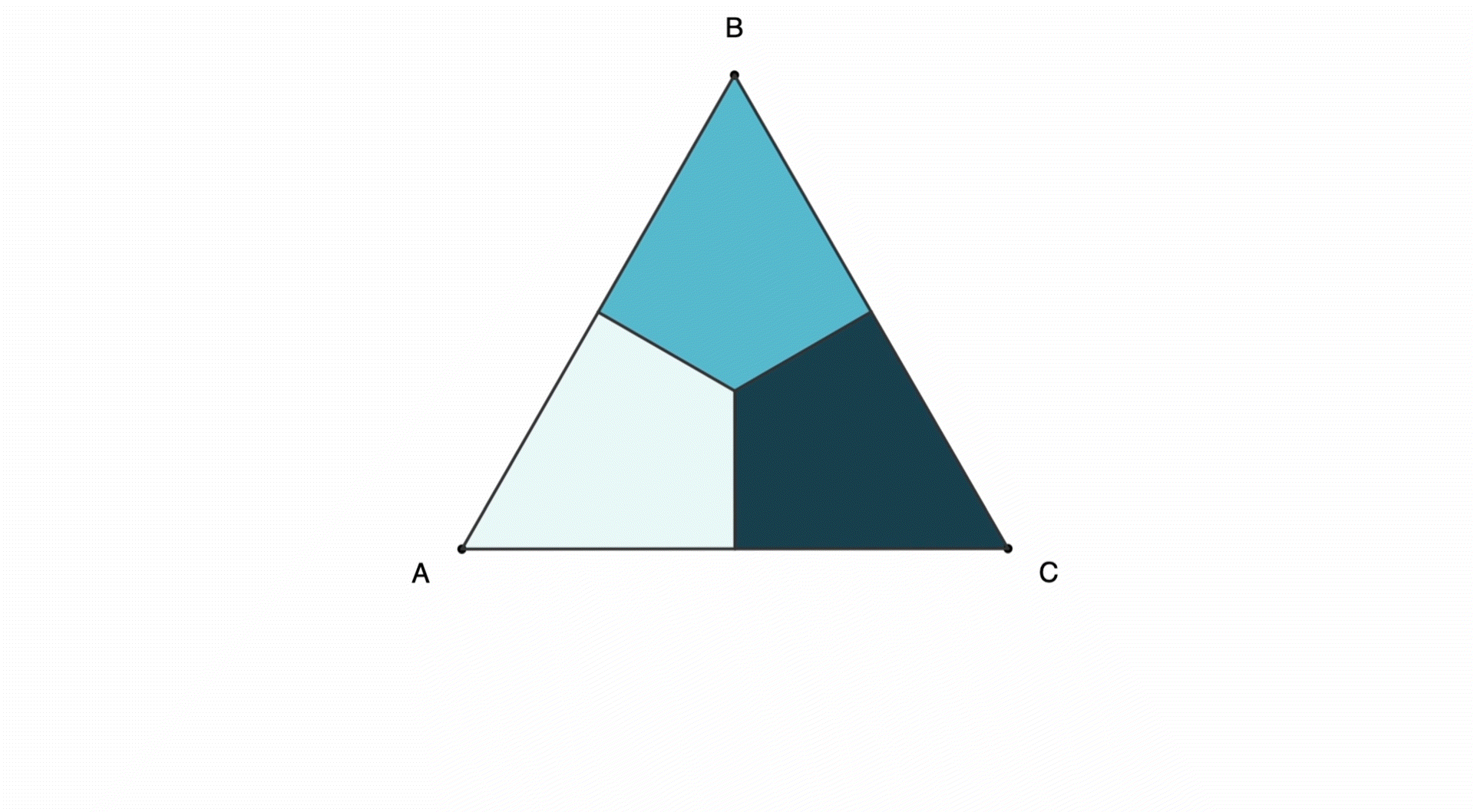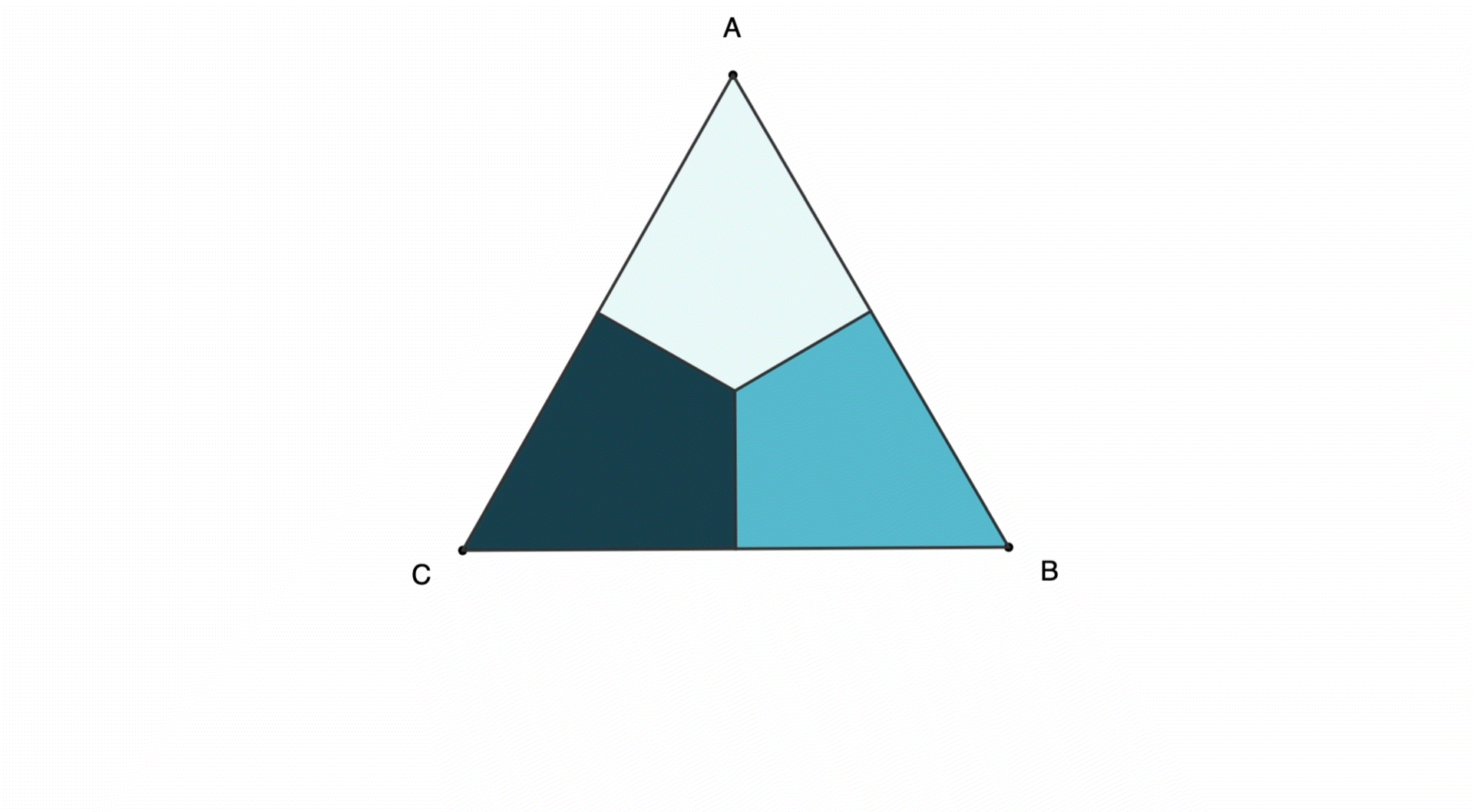
We can also reflect (or flip) the shape horizontally:
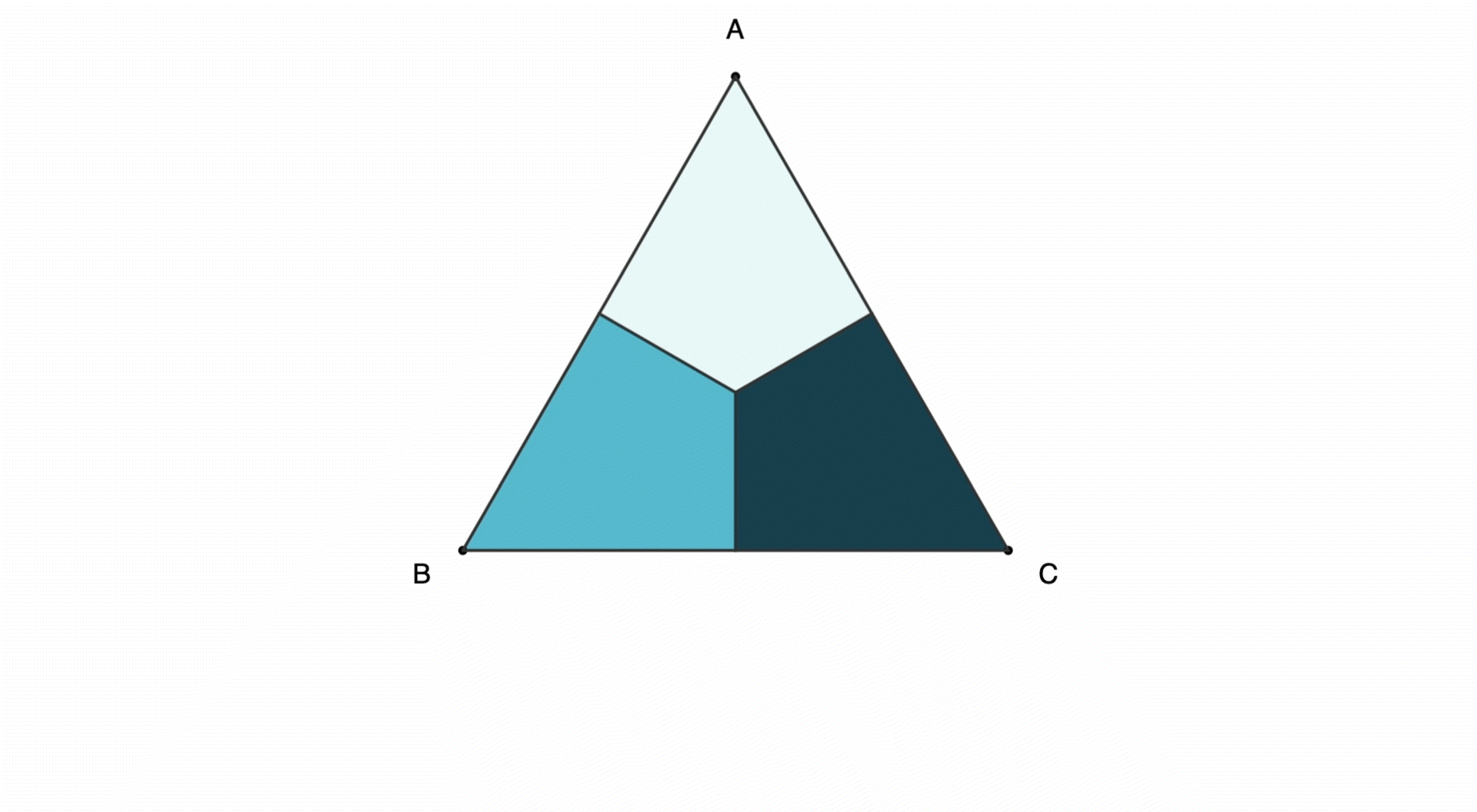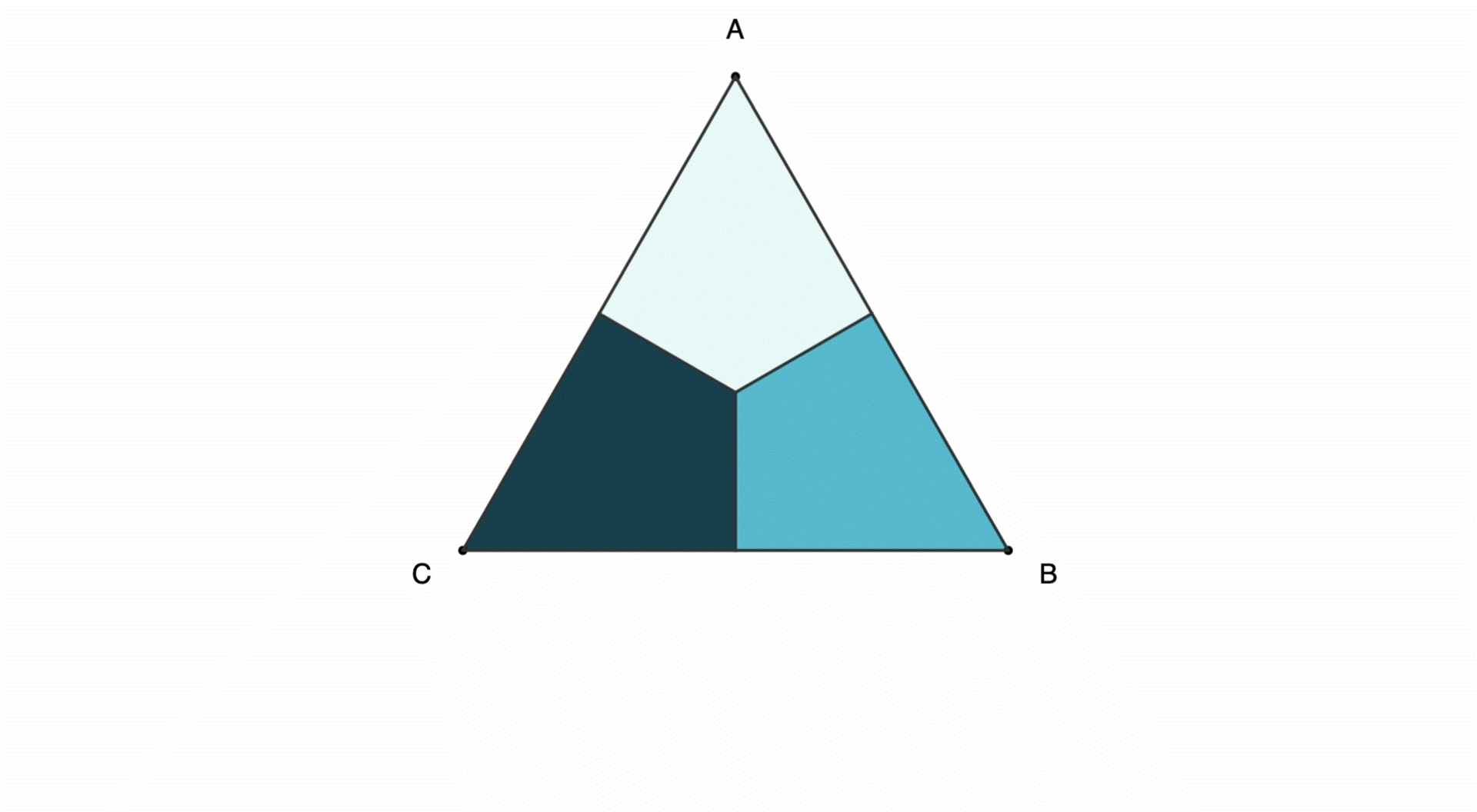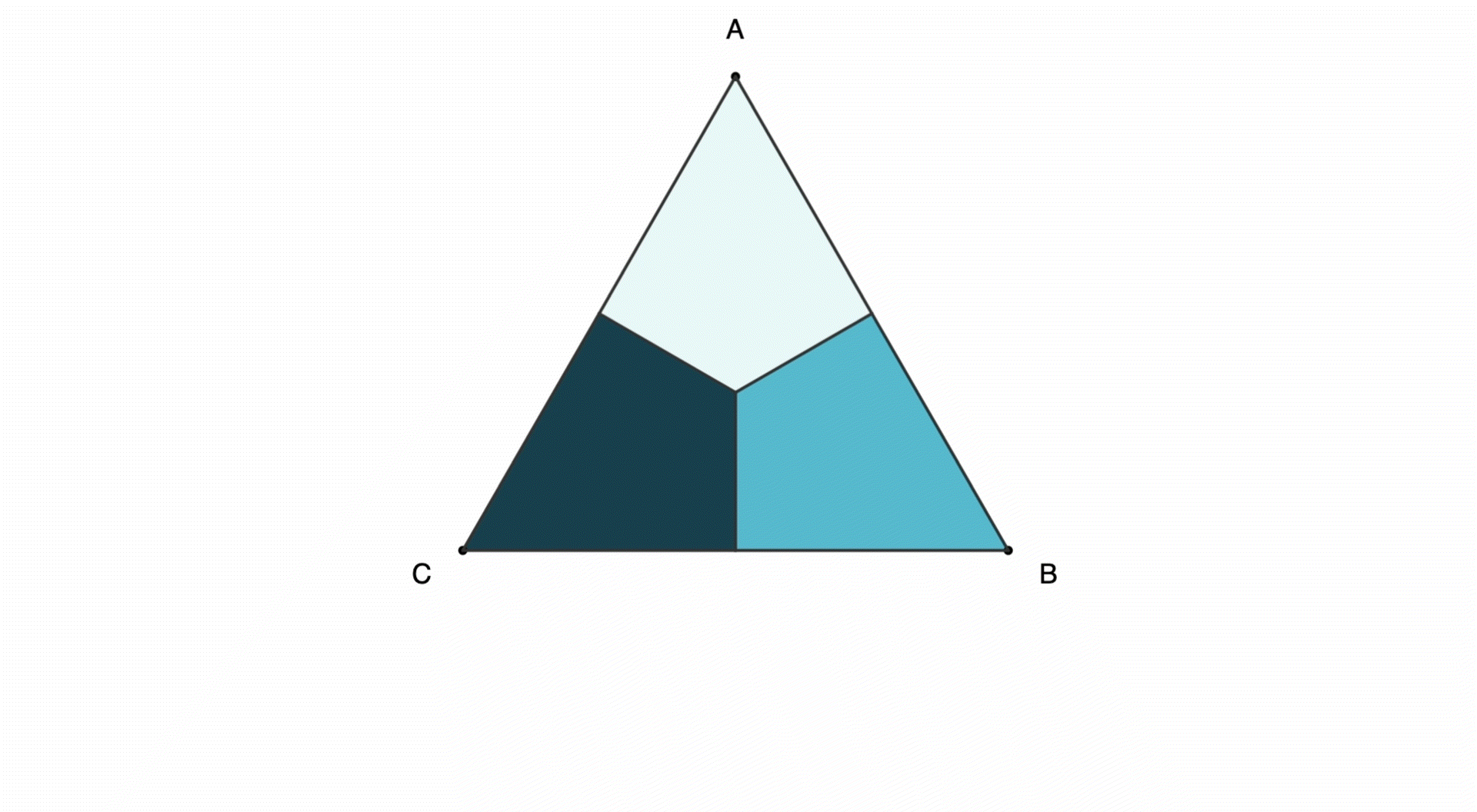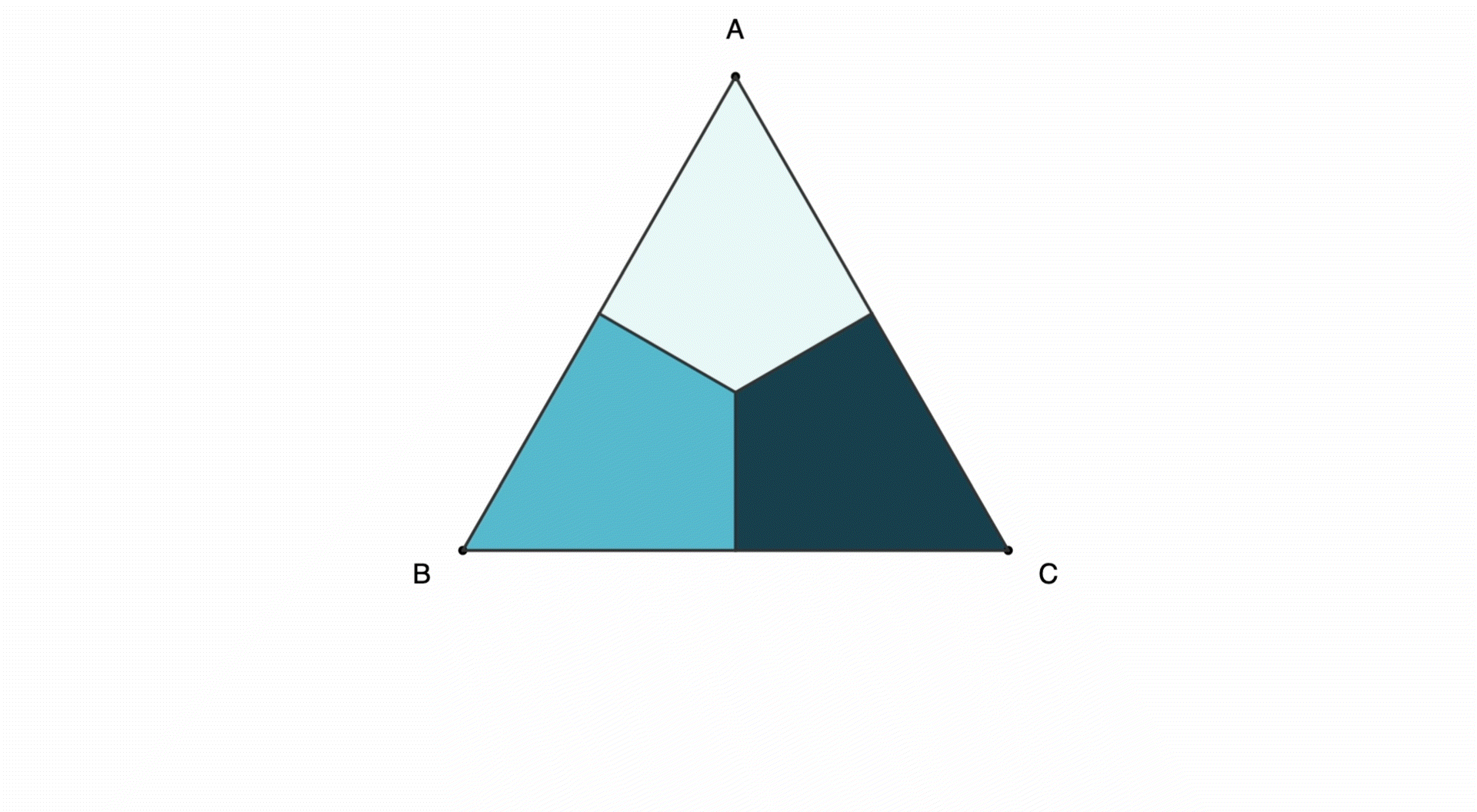
These rotations and reflections can be combined in various ways for triangles and other polygons (full page view):
Activity
Triangles
- How many different configurations can you create using just Rotate and Reflect for a triangle ABC?
- What is the smallest number of moves needed to transform one configuration into any other triangle?
- What conjectures can you form about rotating and reflecting triangles?
Squares
- How many different configurations can you create using just Rotate and Reflect?
- What is the smallest number of moves needed to transform one configuration into any other square?
- What conjectures can you form from your play?
Proofs (optional)
- How could you approach a proof for one of your conjectures?
Educator Resources
Spoiler alert - go play before proceeding (this means you too).
Activity Structure
This is a 45-60 minute activity. For some learners, triangles may be enough for one session - skip squares or save them for later.
Exploration Phase 1 (5-15 minutes)
Playing with triangles
Explore reflecting and rotating the triangles to identify the number of configurations and the number of moves required to obtain each one.
Some of the ways learners may approach this:
- Drawing
- Using the tool and saving images to share on a digital whiteboard.
- Matrices or graphs
- Combinations of rotations/flips and their equivalences
It may be helpful to write the triangles as ABC or [A, B, C] to indicate the order of the vertices, starting from the top and proceeding clockwise.
Conjecture Formation (5-10 minutes)
Allow for time to write down observations and form conjectures. Give examples of conjectures if needed.
Example Conjectures:
Example: "You never need more than 2 moves to go from one configuration to another."
Example: "Flipping and then rotating is the same as rotating twice and then flipping."
Example: "There are 6 possible configurations. "
Triangle Discussion (10-15 minutes)
Share conjectures, observations, and other findings.
There are six possible configurations; share the different ways these were found, along with the reflections and rotations required to obtain them.
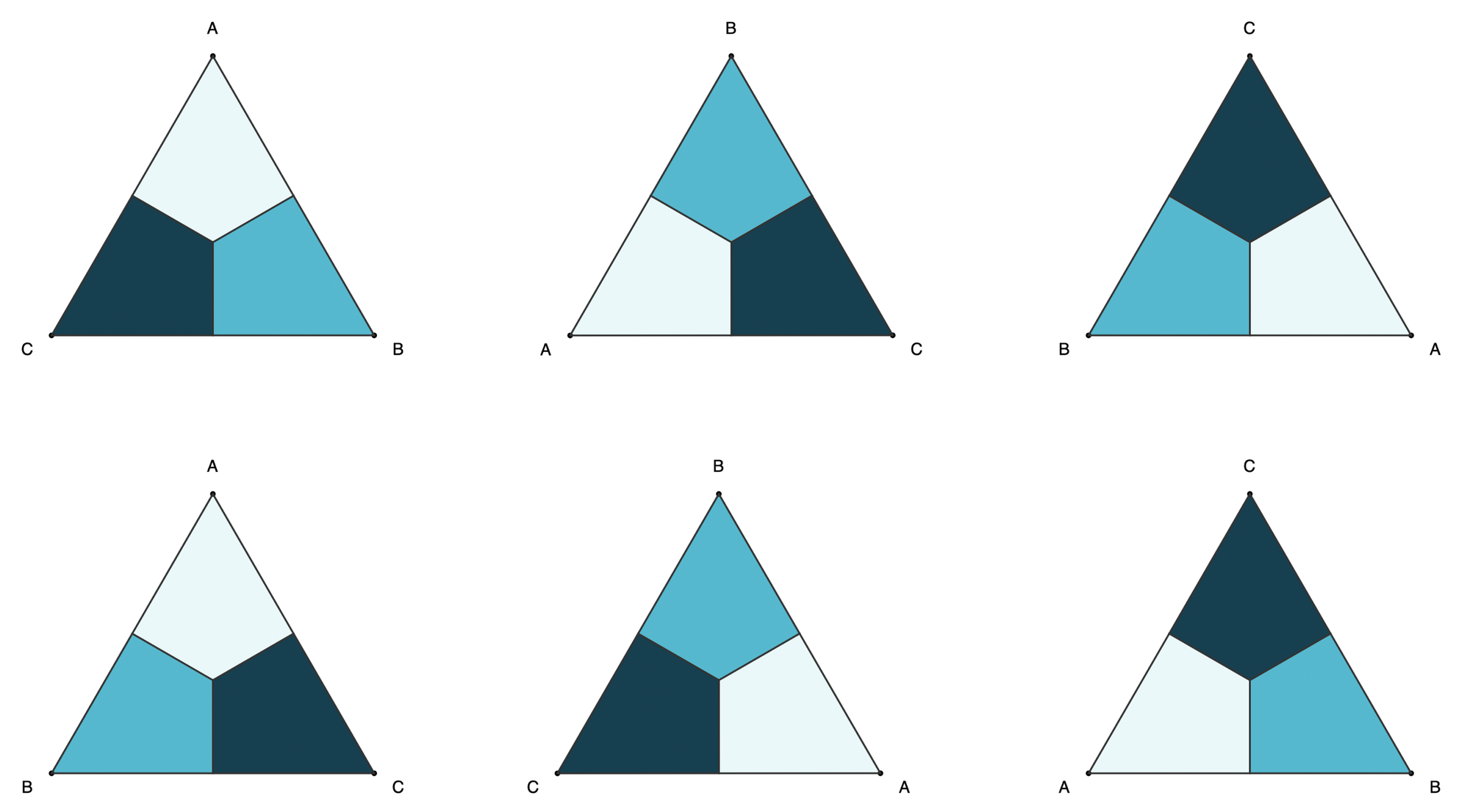
What is the minimum number of reflections and rotations to get to any?
If learners haven't explored combinations of rotations, reflections, and minimum operations, do this as a group:
- Using F for flip/reflect and R for rotate, build the different combinations, results, and equivalencies.
- Does order matter?
- If three moves can be reduced, what does that mean for more moves
- Examples of showing equivalent combinations:
- If FF = identity, then FFR = R and RFF = R.
- If RRF = FR and FRR = RF, then RRFR = (RRF)R = FRR = RF.
- Examples of showing equivalent combinations:
Example of mapping moves to configurations using color:
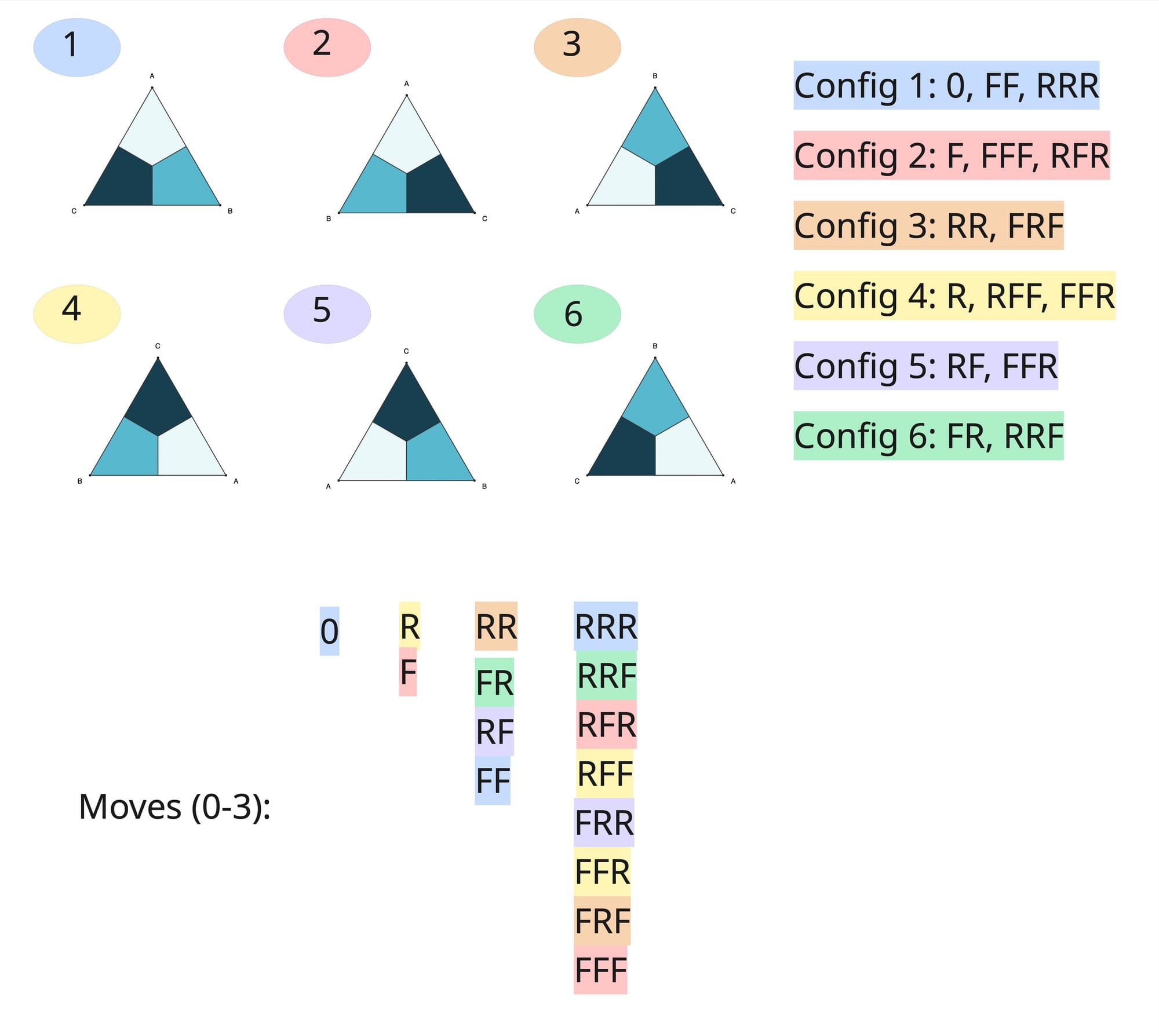
Exploration Phase 2 (5-15 minutes)
Playing with squares
Explore reflecting and rotating the squares to identify the number of configurations and the number of moves required to obtain each one. How is this different than triangles?
If students start exploring the 4! = 24 combinations of letters, provide supporting questions to encourage exploration with flip and rotate moves.
Using reflect and rotate, what configurations are possible?
What do you notice about the diagonals? - (be careful this could give too much away).
It may be helpful to write the squares as ABCD or [A, B, C, D] to show the order of the vertices clockwise from the top-left.
Conjecture Formation (5-10 minutes)
Allow for time to write down observations and form conjectures. Give examples of conjectures if needed.
Example Conjectures:
Example: "You never need more than 3 moves to go from one possible configuration to another."
Example: "There are 8 possible configurations."
Example: "Unlike with a triangle, rotations and flips can't make every combination possible with a square. There are 4!=24, but only 8 possible. "
Example: "Diagonal pairs are preserved with rotations and flips."
Supporting Questions:
- "How do squares and triangles differ with these operations?"
- "Are there any combinations of ABCD that aren't possible with rotations and flips?"
Square Discussion (10-15 minutes)
- Share conjectures.
- Discuss different approaches.
- Compare the findings for the square play with those from the triangle play.
- Share diagonal discoveries.
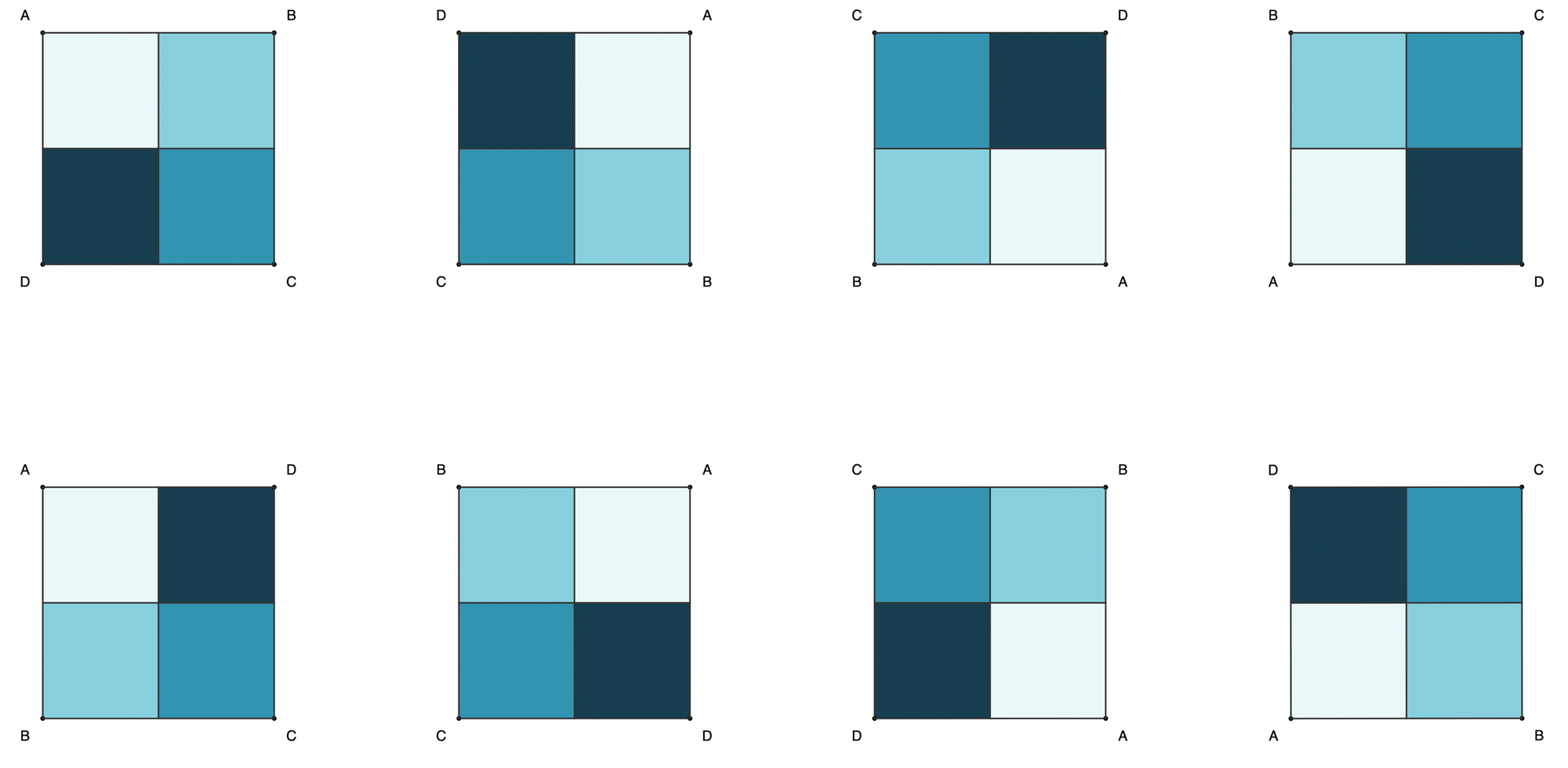
There are eight possible configurations - share the different ways to obtain these and the flips and rotations required.
Optional - Proof Scaffolding
Below are example proof approaches for some of the possible conjectures. These are optional and intended to be conversational, interactive, and flexible, allowing for follow-up inquiries.
Proof-0: There are six combinations possible with three elements, ABC.
- For two elements, A and B, there are two possible arrangements: AB and BA.
- For three elements A, B, and C, we can count systematically by fixing the first position.
- With A first: The remaining positions can be arranged as BC or CB, giving us ABC and ACB.
- With B first: The remaining positions can be arranged as AC or CA, giving us BAC and BCA.
- With C first: The remaining positions can be arranged as AB or BA, giving us CAB and CBA.
- Therefore, there are six total combinations for letters A, B, and C.
Proof-1: Six configurations for triangle ABC can be obtained with rotations and horizontal reflection, and only two moves are needed to get any of them.
![Six possible triangles from horizontal reflection and rotations showing vertices and light, medium, and dark regions of the triangles. The possibilities are ABC, BCA, CAB, ACB, BCA, CBA and are labeled as [A,B,C], etc.](https://www.fractalkitty.com/content/images/2025/07/image-2.png)
- There are 3! = 6 possible combinations for a triangle ABC (see Proof-0).
- All six combinations can be obtained with F = Horizontal Reflect/Flip and R = CW Rotate:
- [A,B,C] = 0 (no move)
- [A, C, B] = F
- [B, C, A] = R
- [B, A, C] = F + R
- [C, A, B] = R + R
- [C, B, A] = R + F
- All six combinations are configurations that can be obtained using rotation and horizontal reflection.
- Every configuration is obtainable in at most two moves (see step 2 above).
- The 2-move sequences RR, FR, and RF cannot be reduced to fewer moves, since the complete set of sequences with ≤1 moves {0, F, R } produces different configurations.
- Therefore, no more than two moves are needed to obtain any configuration.
Proof 2: Eight configurations for square ABCD can be obtained with rotations and horizontal reflection, and only three moves are needed to get any of them.
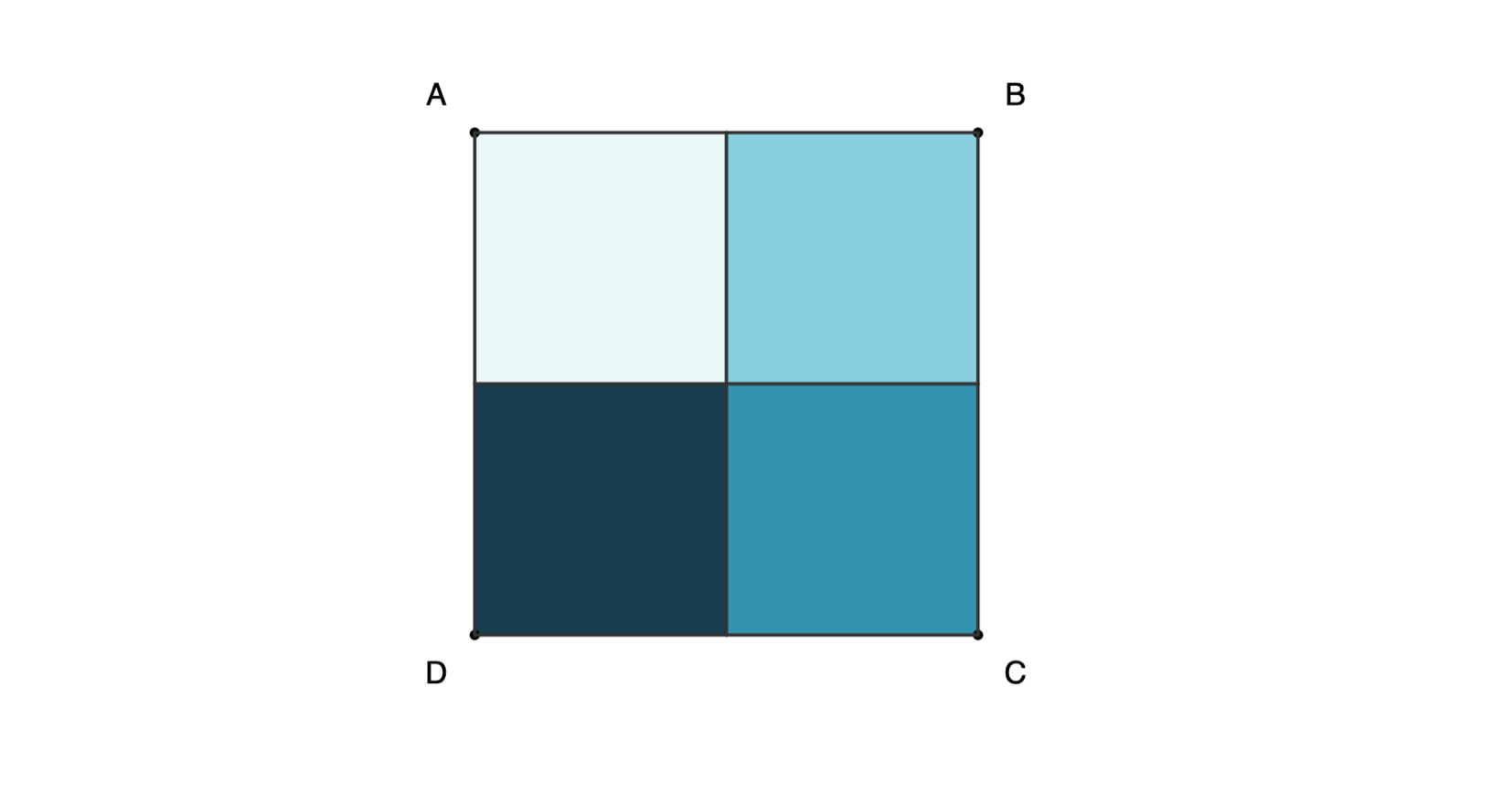
- We can represent a square ABCD as a sequence of letters with vertices labeled in a clockwise direction.
- For a square ABCD, flipping and rotating the shape preserves diagonal pairs AC and BD.
- There are 4! = 24 possible combinations of the letters ABCD.
- ABCD, ABDC, ACBD, ACDB, ADBC, ADCB, BACD, BADC, BCAD, BCDA, BDAC, BDCA, CABD, CADB, CBAD, CBDA, CDAB, CDBA, DABC, DACB, DBAC, DBCA, DCAB, DCBA
- Valid combinations will not have AC or BD next to each other to preserve diagonals.
- Only 8 of the 24 possible combinations preserve the diagonals:
- Valid (8): ABCD, ADCB, BADC, BCDA, CBAD, CDAB, DABC, DCBA
- Invalid (16): ABDC, ACBD, ACDB, ADBC, BACD, BCAD, BDAC, BDCA, CABD, CADB, CBDA, CDBA, DACB, DBAC, DBCA, DCAB
- The eight configurations can be obtained with the following rotations and flips:
- [A, B, C, D] = 0 (no move)
- [A, D, C, B] = R + F
- [B, A, D, C] = F
- [B, C, D, A] = R + R + R
- [C, B, A, D] = F + R
- [C, D, A, B] = R + R
- [D, A, B, C] = R
- [D, C, B, A]=F + R + R
- Eight configurations can be obtained by rotating and reflecting the square ABCD.
- Every configuration is obtainable in at most three moves (see step 6 above).
- The 3-move sequences RRR and FRR cannot be reduced to fewer moves, since the complete set of sequences with ≤2 moves {0, F, R, RF, FR, FF, RR} produces different configurations than RRR and FRR. (Note that FF gives the same configuration as no move.)
- Therefore, no more than three moves are needed to obtain any configuration.
Tools and Supplies
- Paper, pencils, or a whiteboard.
Vocabulary
- Conjecture: A mathematical statement that is believed to be true but has not yet been proven.
- Configuration: A specific arrangement of labeled vertices on a geometric shape.
- Transformation: An operation that changes the position or orientation of a shape (like rotation or reflection).
- Rotation: Turning a shape around a fixed center point by a specific angle.
- Reflection/Flip: Creating a mirror image of a shape across a line.
- Permutation: An arrangement of objects in a specific order.
- Diagonal: A line segment connecting two non-adjacent vertices of a polygon.
- Dihedral group: The mathematical group describing all possible rotations and reflections of a regular polygon.
- Identity: The "do nothing" transformation that leaves a shape unchanged.
- Inverse: A transformation that undoes another transformation.
- Group theory: The mathematical study of symmetries and transformations.
- Proof by construction: Proving a statement by explicitly building or showing all examples.
- Upper bound: The maximum possible value in a given context.
- Lower bound: The minimum required value in a given context.
- Reduction: Simplifying a sequence of operations to its shortest equivalent form.
- Equivalence: When two different sequences of operations produce the same result.
- Clockwise: Moving in the same direction as the clock hands.
Extensions and What Ifs
- What about pentagons or hexagons? How many configurations are reachable? What's the maximum number of moves needed? (The tool above has more polygons.)
- What does this look like if we create different operations? Be imaginative.
- 3D extensions: What happens with tetrahedra, cubes, or other 3D shapes?
- Rubik's cube and other puzzle cube connections: Do the same principles apply to understanding solutions?
Additional Resources
Image Files:
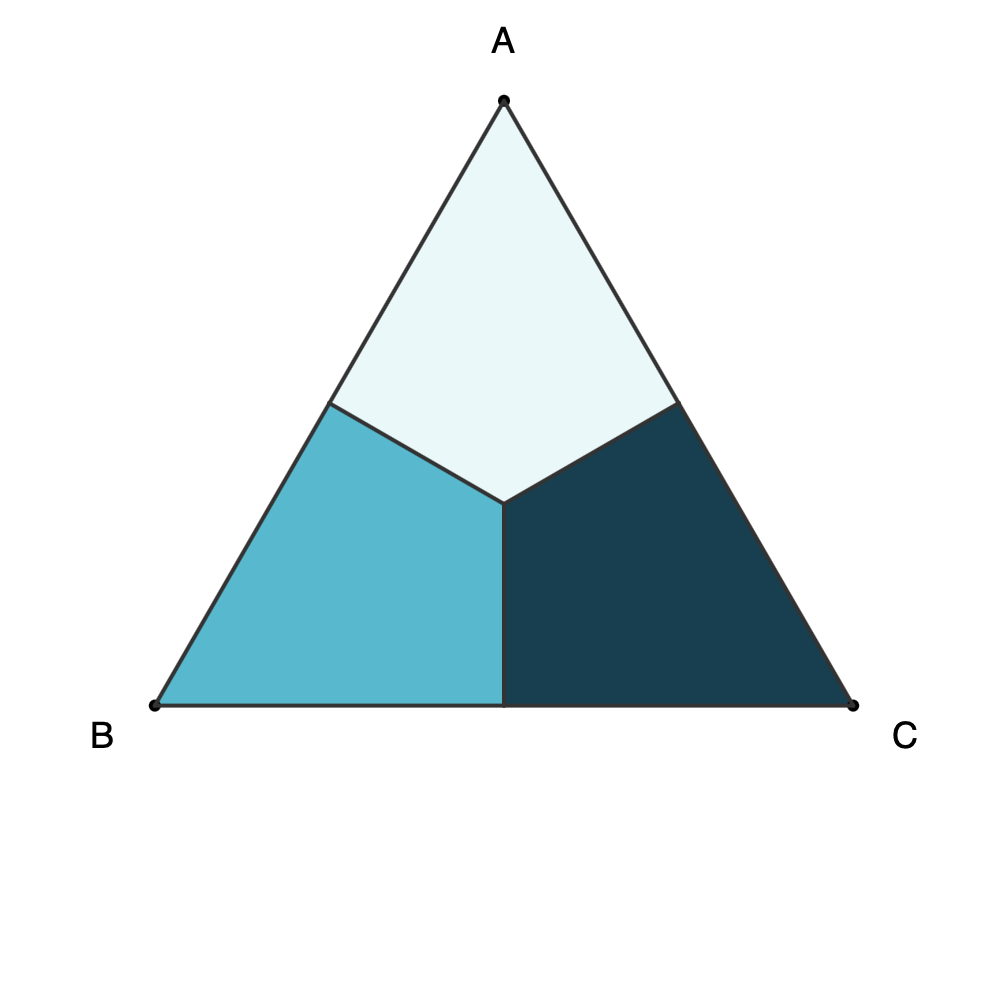
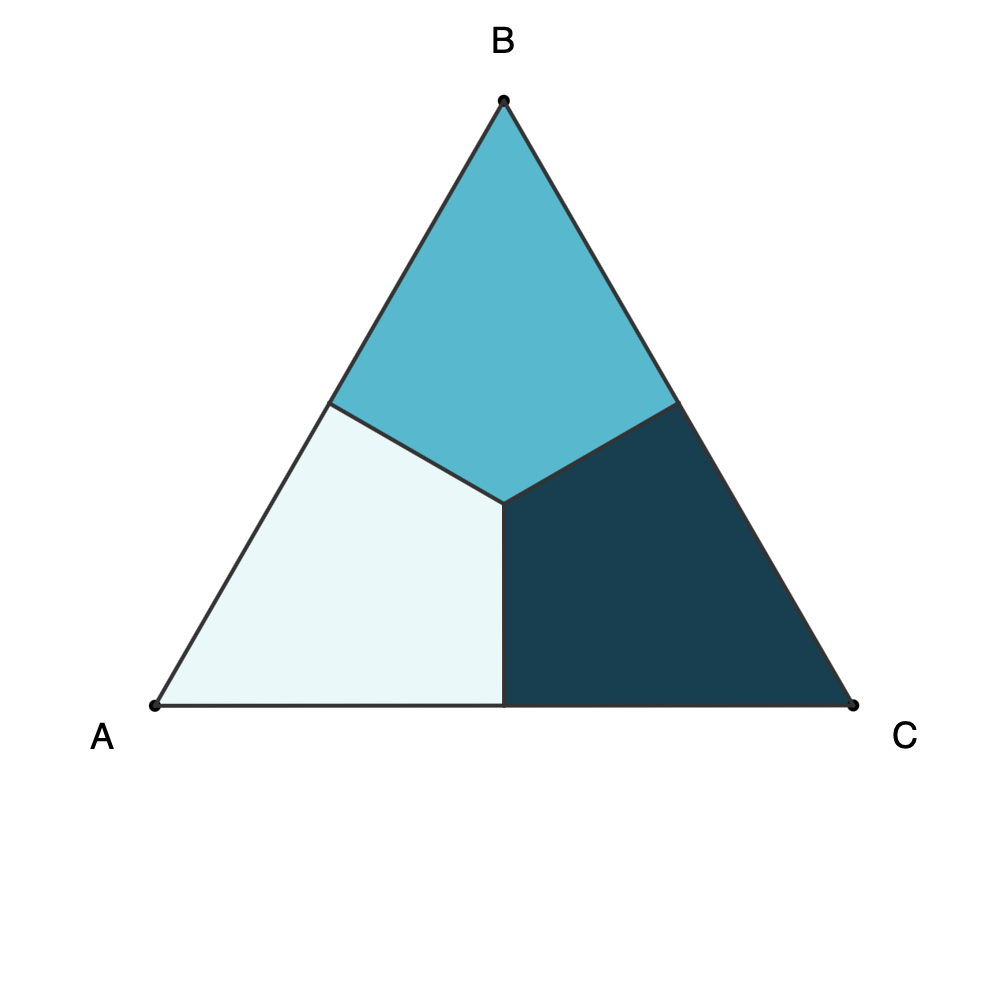
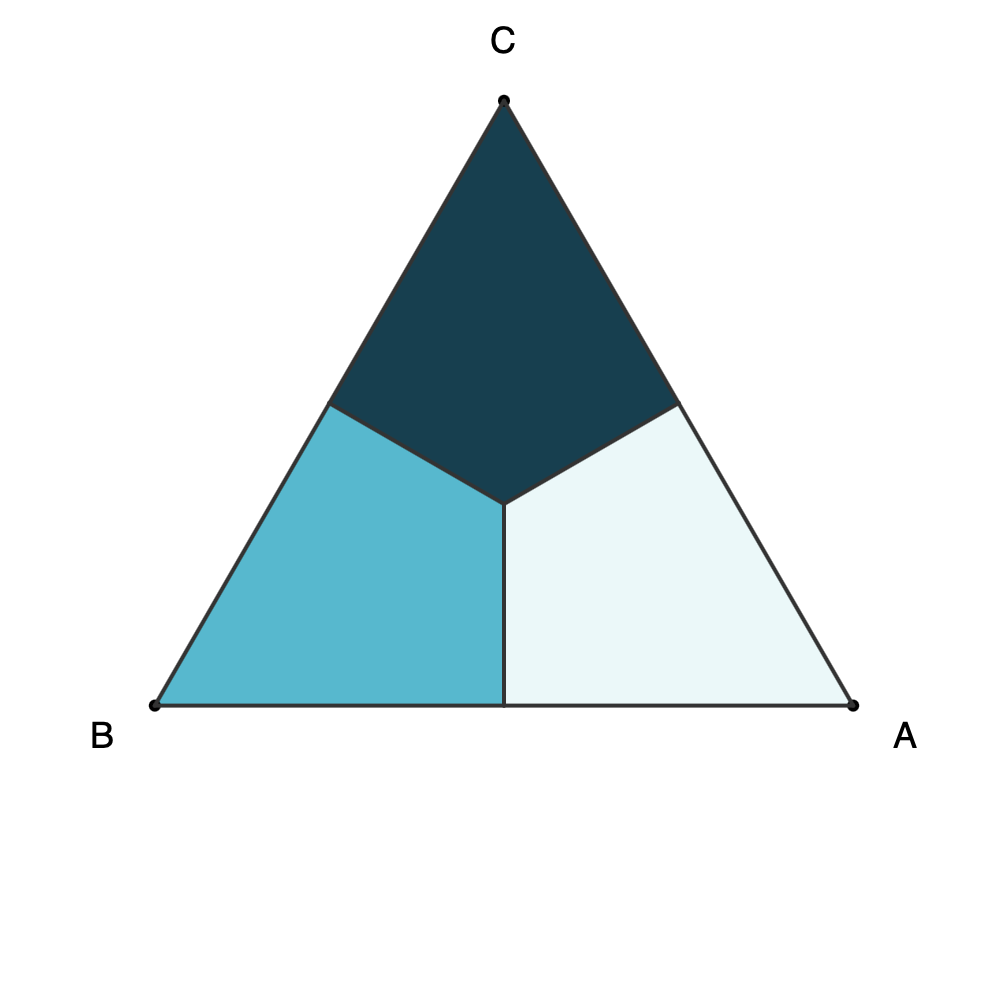
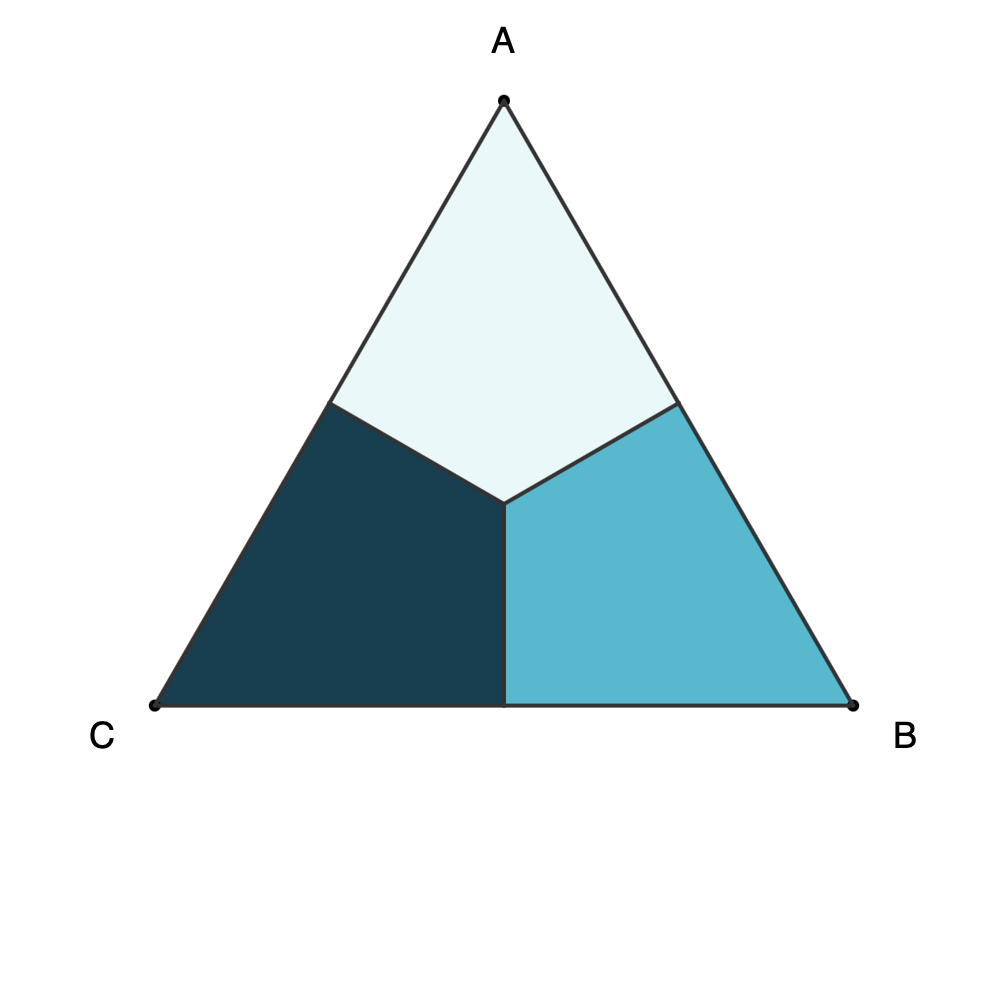
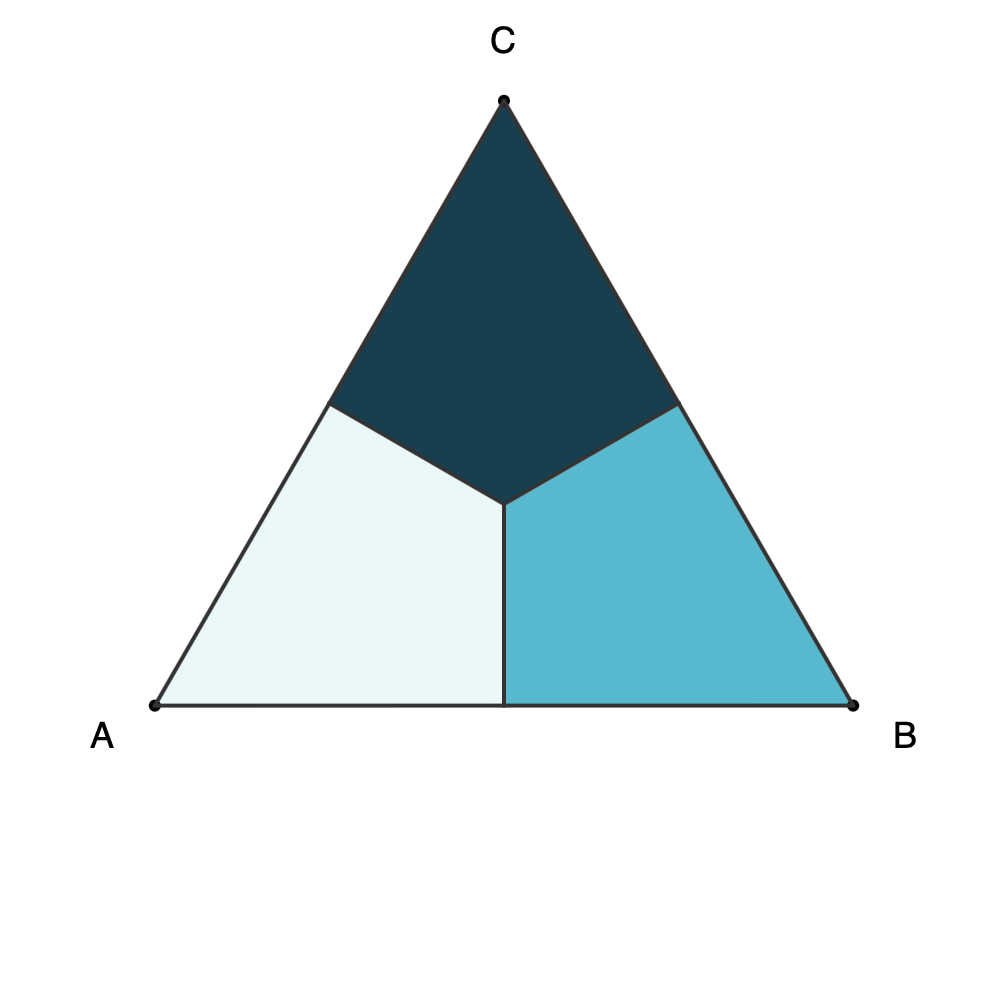
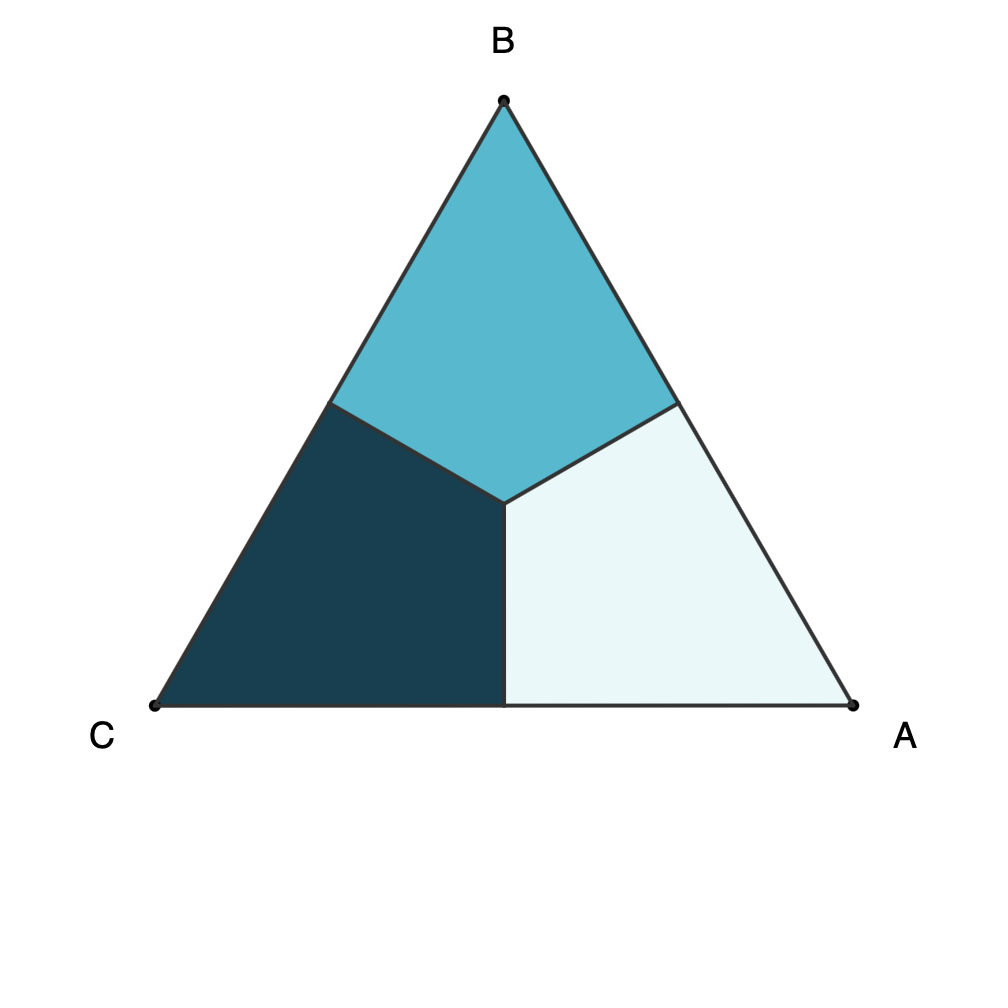
Triangle configurations as separate files
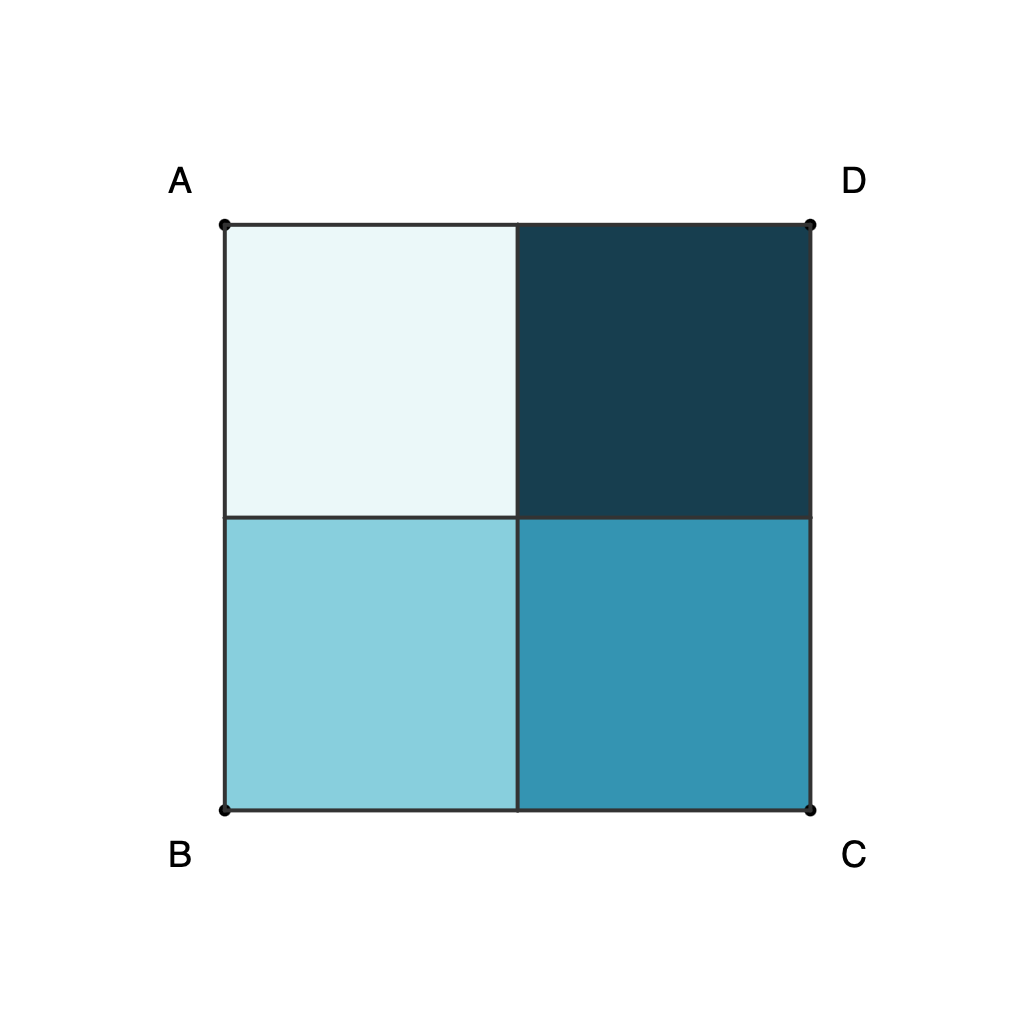
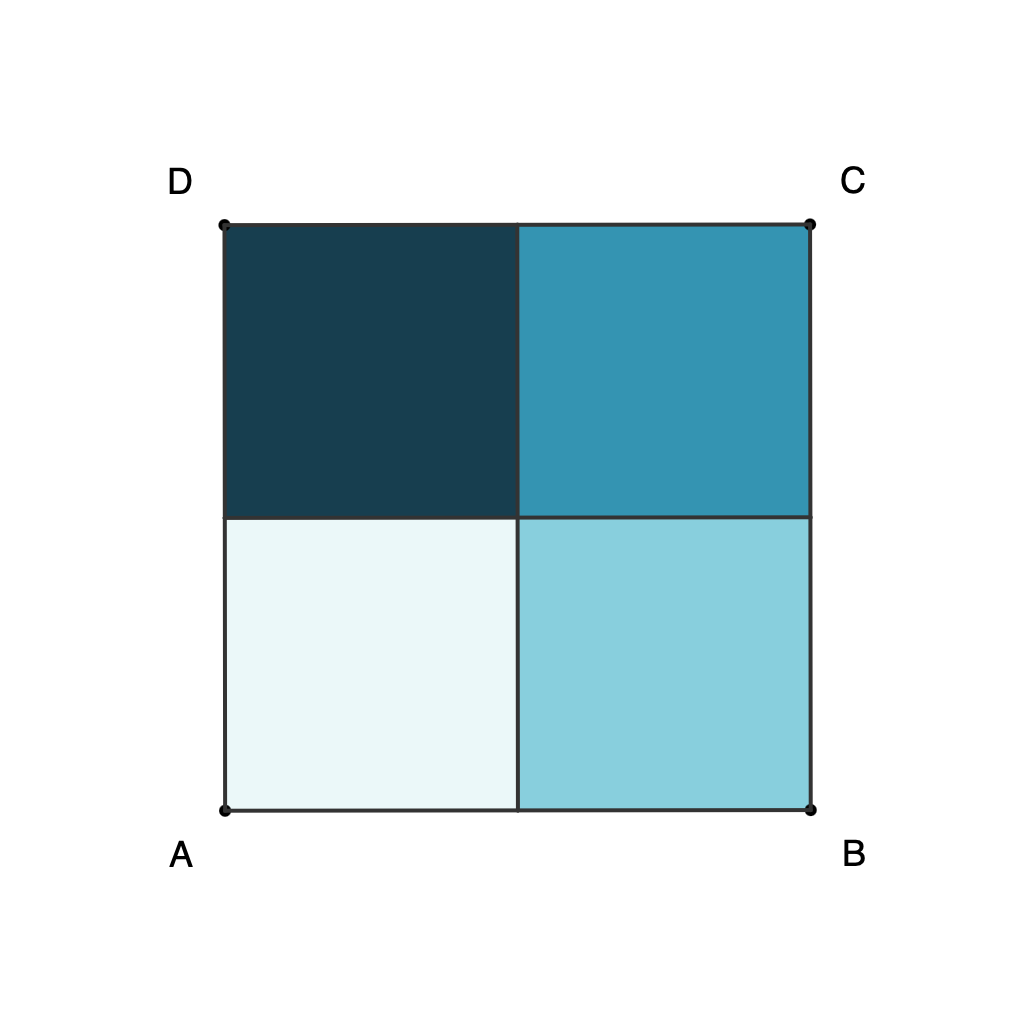
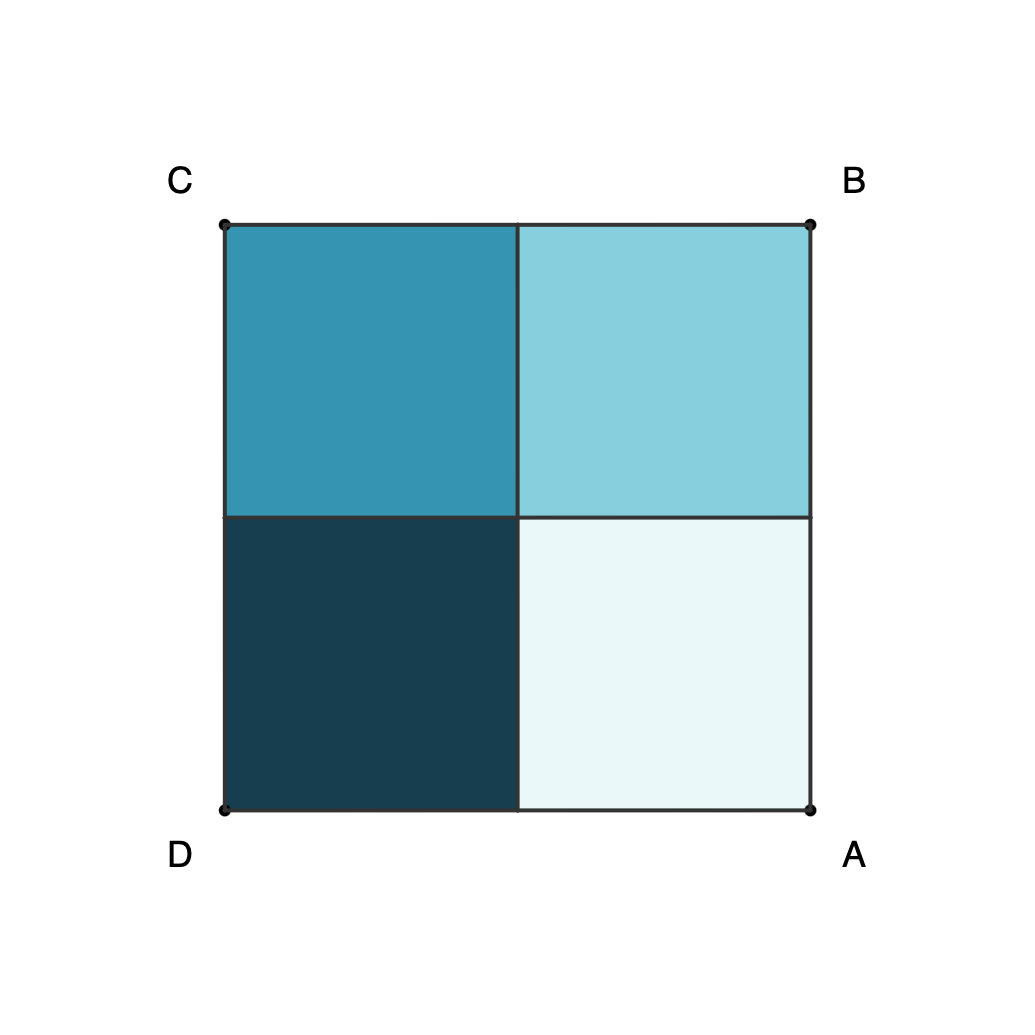
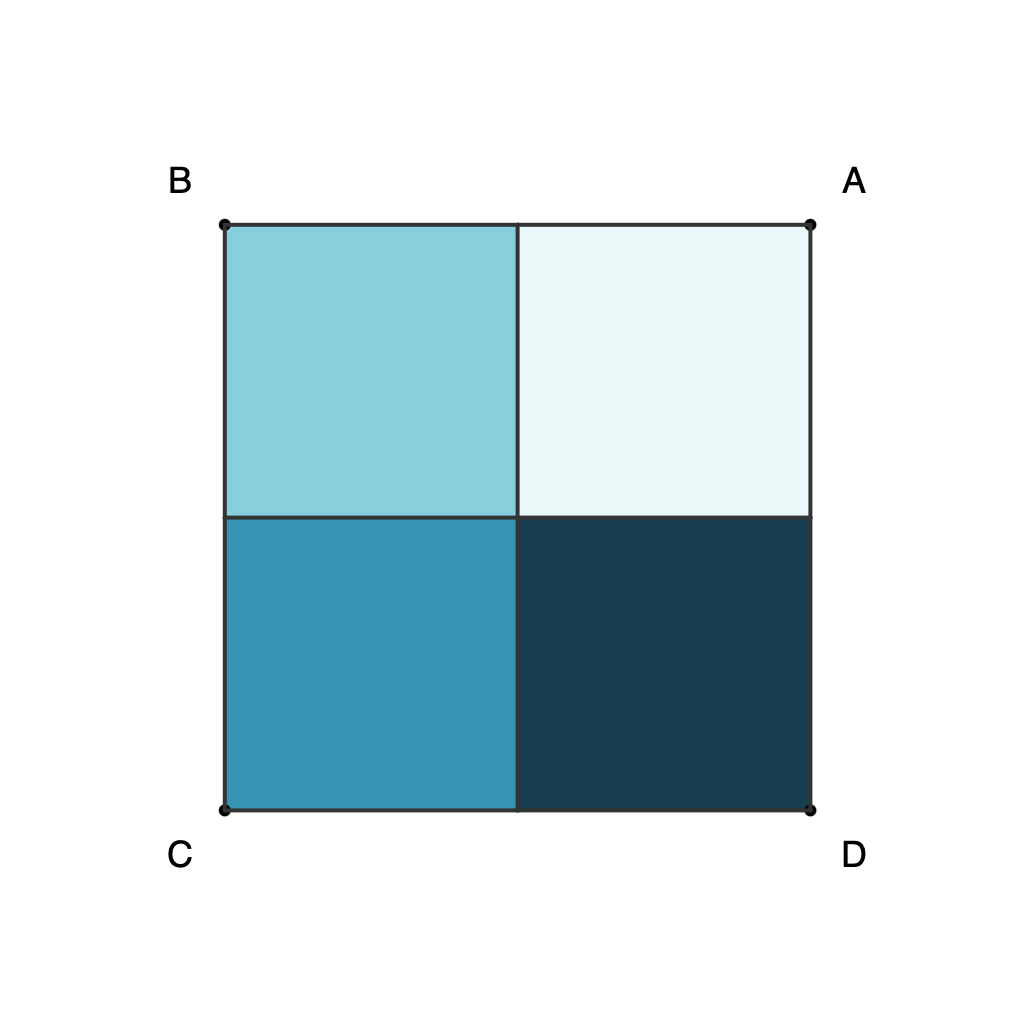
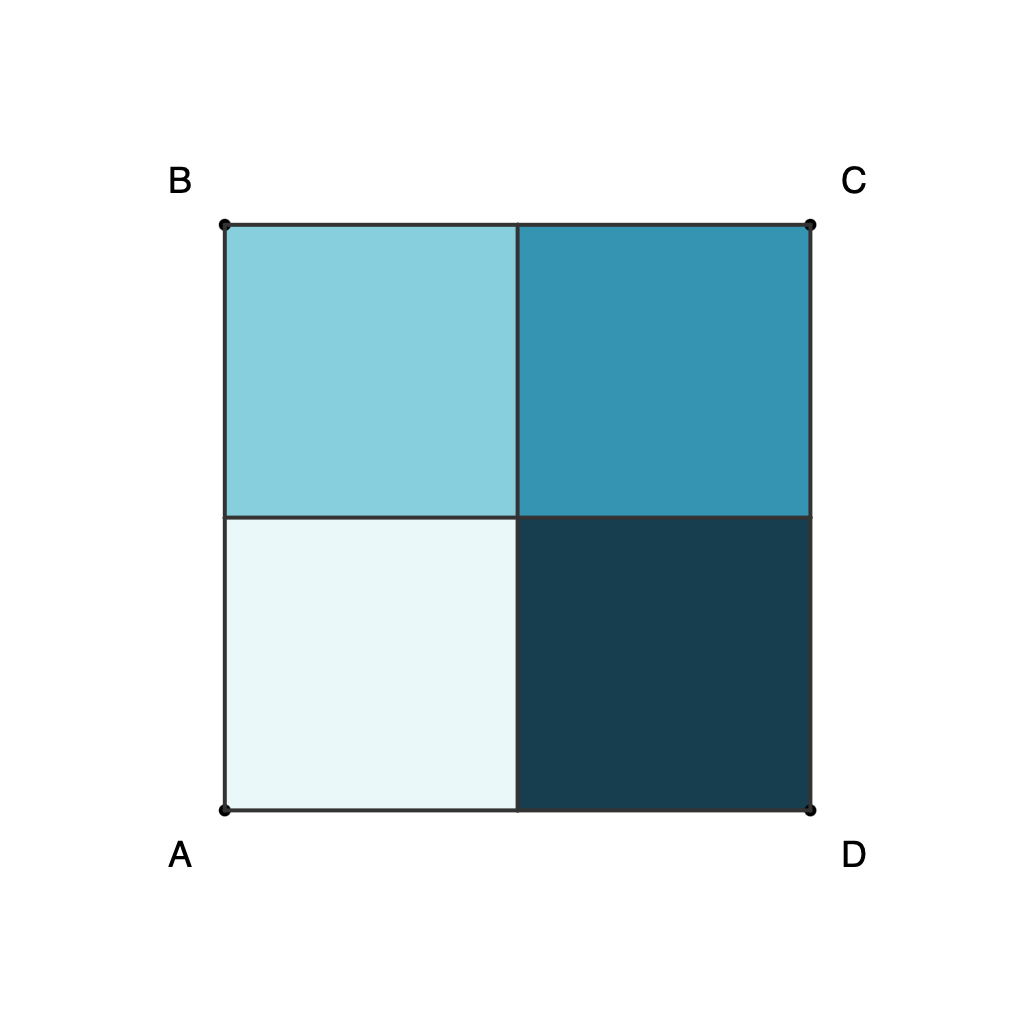
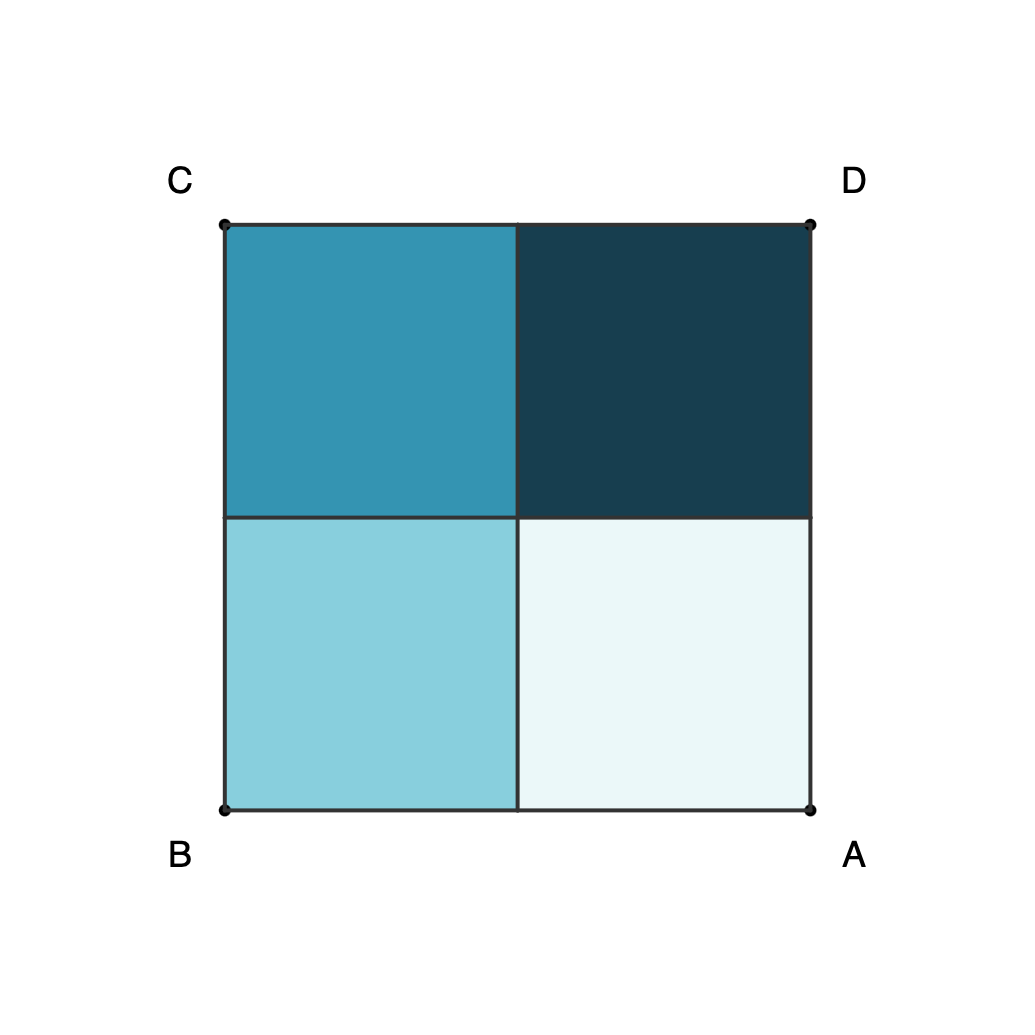
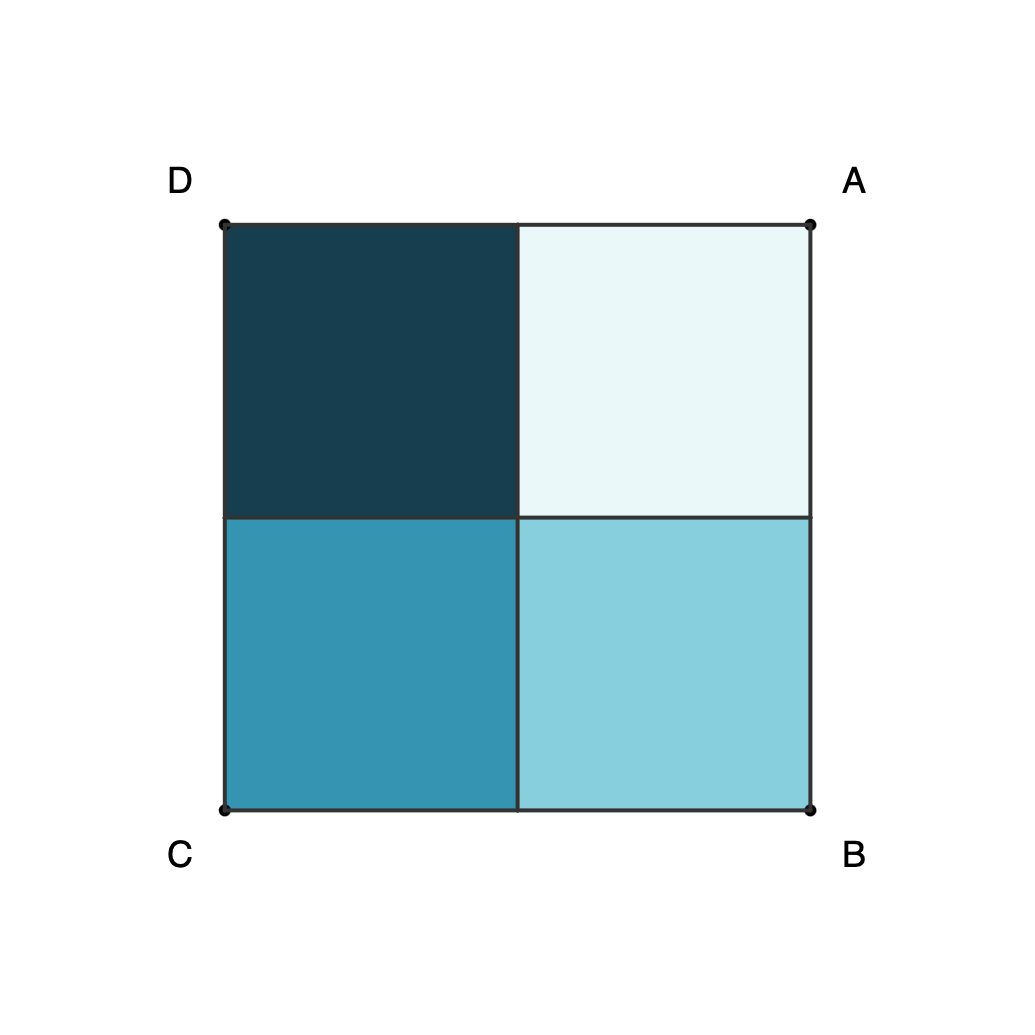
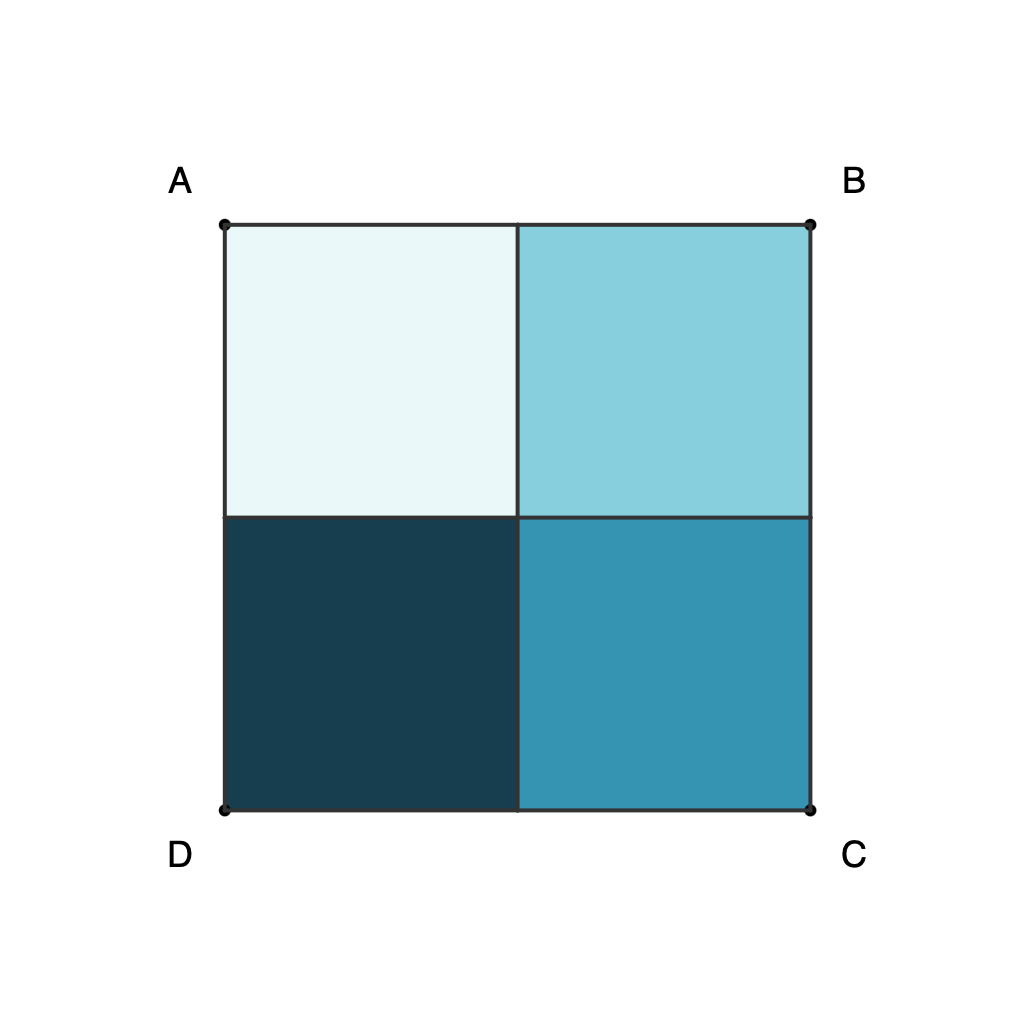
Square combinations as separate files

