This is the first of a series of guided inquiries in math. If a document is preferred over a blog post, the pdf file is below:

Introduction

When circles overlap they make lunes:

or lenses:

or other fun shapes:

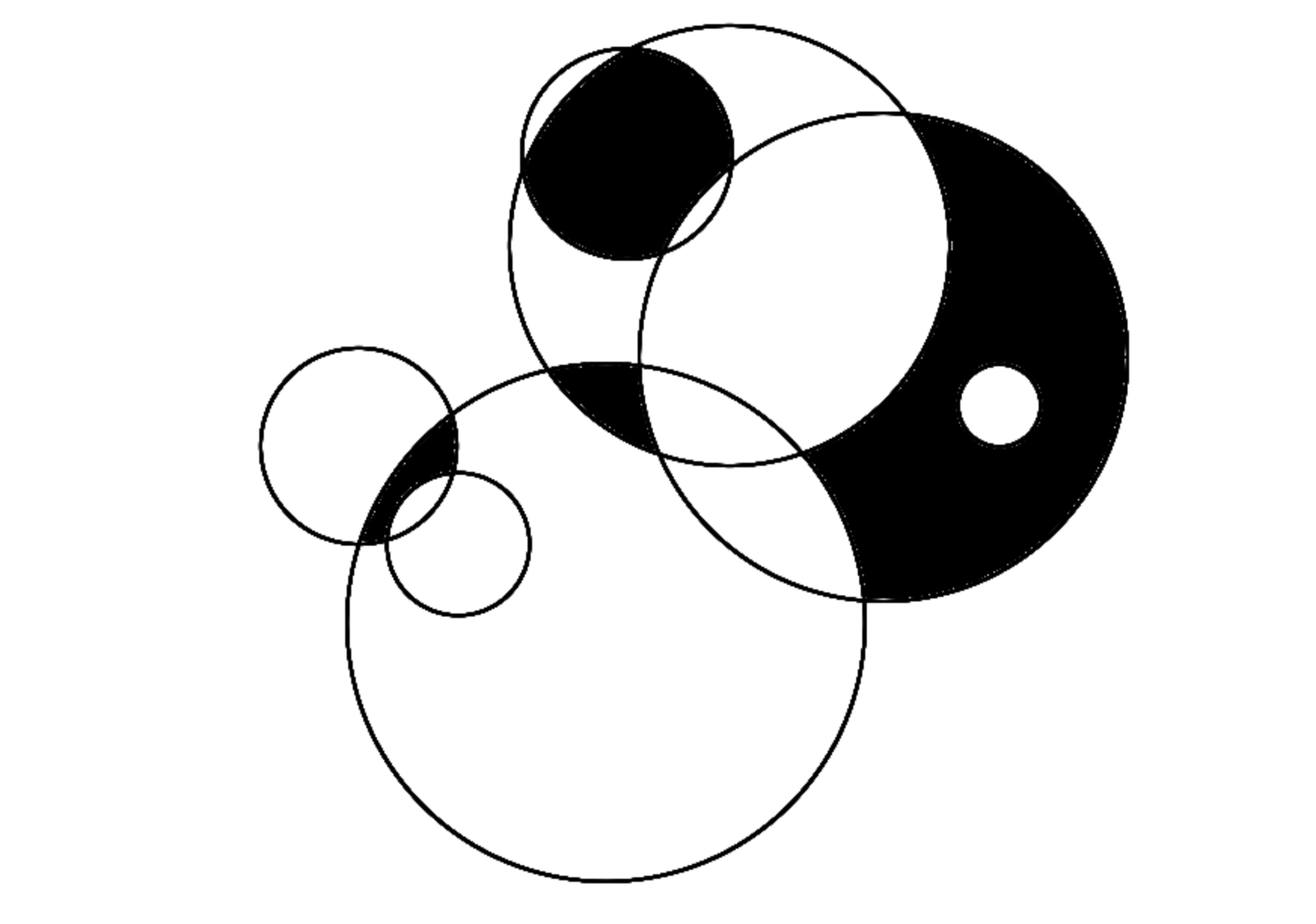
Activity

Let's play with how we color circles that overlap.

First, draw a few circles on a page. Make their intersections distinct.

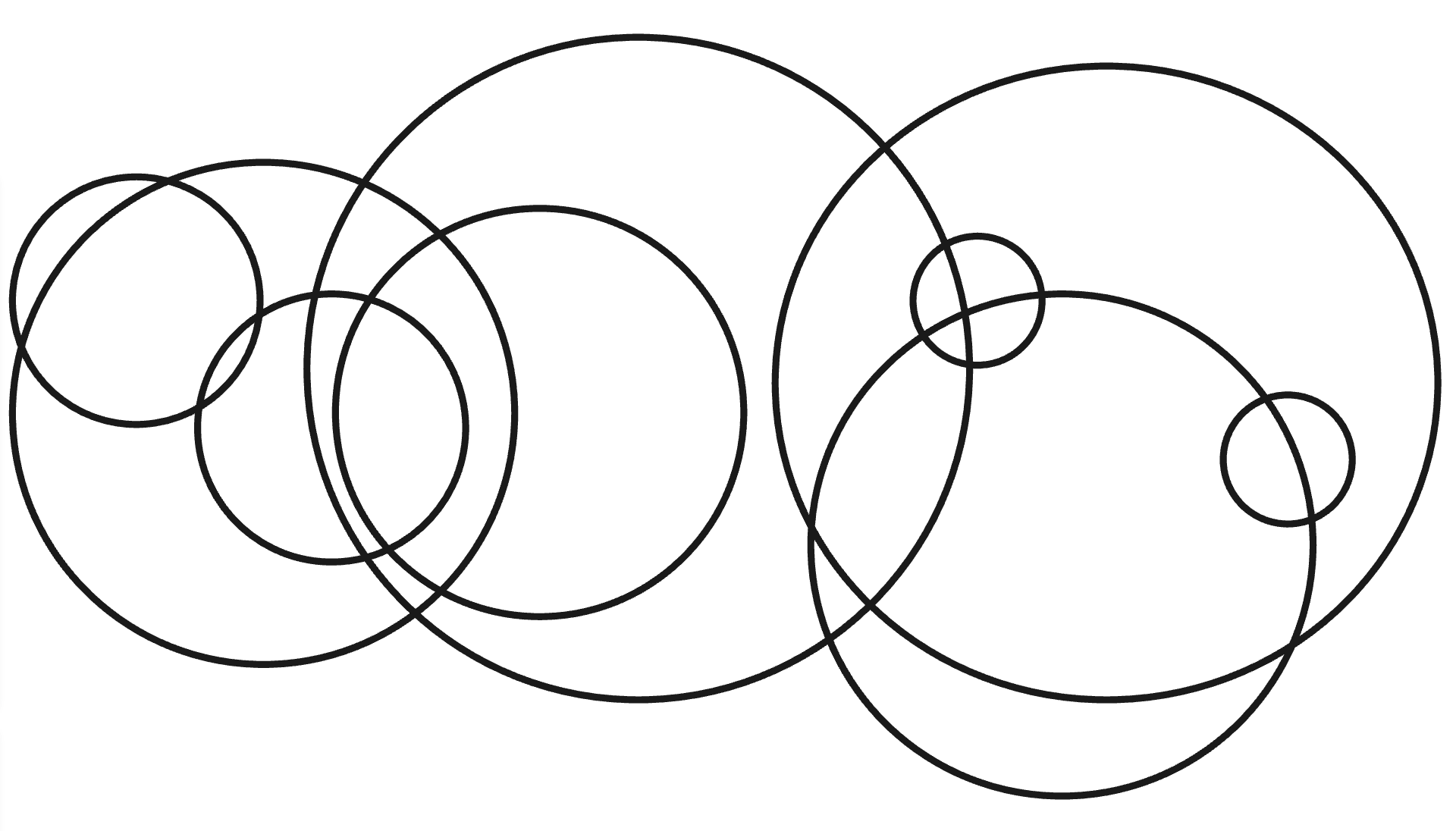
Challenge

• Color the regions so no adjacent regions share the same color.
• Discover the minimum number of colors needed.
• Form a conjecture that can be used to determine each region's color.
• Test your conjecture.
• Bonus: What would a proof look like?

Activity Structure

This is a 45-60 minute activity to explore developing conjectures with visual patterns.

Exploration Phase (5-10 minutes)

Give time to color and draw circles to form ideas. If there is any confusion on the task - give an example that uses many colors: (Here is a tool to play - also full page option).

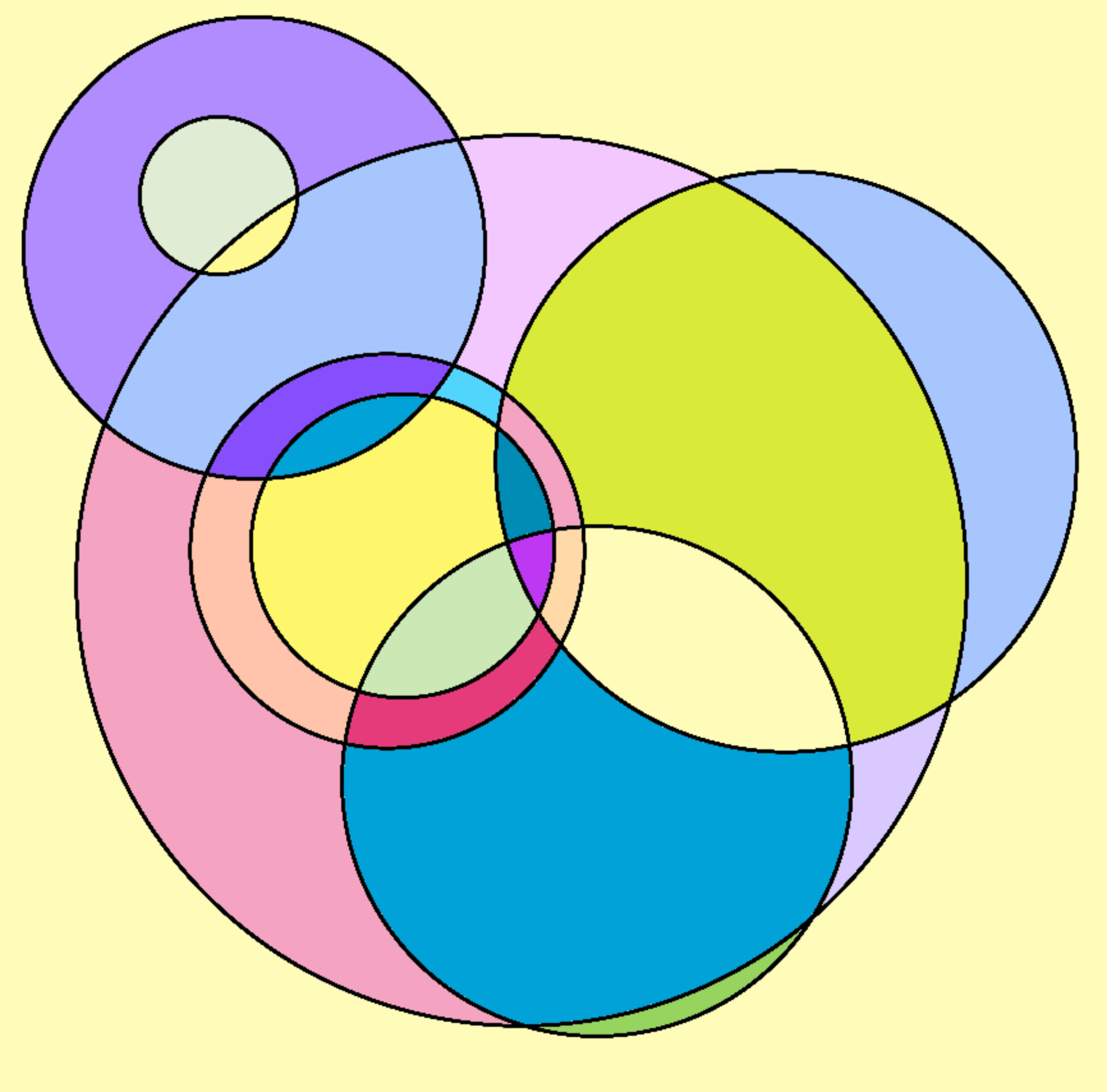
Conjecture Formation (5-10 minutes)

Allow for time to write down observations and form conjectures. Give examples of conjectures if needed. There are two questions to answer here:

• What is the minimum number of colors needed?
• What rule can be used to determine each region's color?

Example: "A graph of overlapping distinct circles needs ____ colors so that no two adjacent regions have the same color."

Example: "Any region's color can be determined by <insert rule>."

Supporting Questions:

• "What do you notice about regions that share a boundary?"
• "When you cross a circle boundary, what happens to the count of circles containing the region?" (this question can give it away)
• "Can you find any arrangement where three colors are necessary?"

Discussion and Discovery (10-15 minutes)

• Share conjectures.
• Discuss different approaches.
• Guide learners toward the even-odd insight if they don't discover it.
  • Induction is a good approach for this - start with one circle, then two, etc.
  • Add questions as needed to start thinking of how many circles contain a region.
• Once a two-color conjecture is found, here is a tool to play with parity flipping.

Example Student Conjectures

• "Two colors are needed."
• "The color depends on how many circles contain the region."
• "Two colors are sufficient for coloring regions formed by overlapping circles."
• "Color regions based on whether they are contained in an even or odd number of circles."
• "Overlapping circles can be represented with a bipartite graph."

Possible Misconceptions

• "The number of colors equals the number of regions."
• "Four colors are needed."

Optional - Proof

Overview

The key insight is that as you cross any circle boundary, you either enter or exit exactly one circle. This changes the parity (odd/even) of the number of circles containing that region. Therefore, adjacent regions must have different parities, which means they can be colored with just two colors.

• Here is a tool to show parity flipping and play once the two color conjecture is found.
• Using a whiteboard for each step is useful.

Leading Induction Questions

• With 1 circle, how many regions? How many colors are needed?
• Induction hypothesis: Assume two colors work for n circles.
• Inductive step: What happens when we add circle n+1?
• How does this new circle affect the existing regions?
• Does the coloring rule still work? Why?

Example Proof:

For any arrangement of circles with distinct intersections:

1. When crossing any circle boundary, we move from one region to an adjacent region.
2. The number of circles containing the region changes by exactly ±1.
3. Therefore, adjacent regions must have opposite parities.
4. If we give even parities one color and odd parities another, no two adjacent regions share a color.
5. Therefore, exactly two colors are necessary to color any arrangement of circles with distinct intersections.

Tools and Supplies

This can be done virtually, on paper, or with code.

• On paper:
  • crayons/markers
  • paper
  • compass - optional (circles don't need to be perfect)
• Digital Drawing tools:
  • In browser circle paint(on codepen) or on this site here.
  • Online whiteboards (miro, figma, etc) - participants can mark regions color without coloring in all the way
• Coding - (not a 60 min activity)
  • Coding is not a single session activity and is more of a prompt to then go contemplate.
  • P5js, python, shaders or other languages can be used to figure out the algorithm.

Vocabulary

• Lune: A crescent-shaped region formed when one circle partially overlaps another.
• Lens: The almond-shaped region where two circles overlap.
• Adjacent regions: Regions that share a boundary segment.
• Chromatic number: The minimum number of colors needed to properly color a set of regions.
• Bipartite graph: A graph whose vertices can be divided into two groups with no edges connecting vertices within the same group.
• Parity: The property of being even or odd.
• Conjecture: A mathematical statement that is believed to be true but has not yet been proven.
• Counterexample: A specific example that disproves a conjecture.
• Even-odd rule: The principle that regions can be colored based on whether they're contained in an even or odd number of circles.
• Invariant: A property that remains unchanged under certain operations (such as going from one region to another and changing parity).
• Boundary: The line or curve that separates two regions.
• Intersection: The place where two or more circles overlap.
• Region: A connected area bounded by circle arcs and/or the unbounded exterior.

Extensions and What Ifs

1. Graph Representation: Create a graph where each region is a vertex, and regions sharing a boundary are connected by edges. What does this graph look like? How does this relate to the chromatic number? (Bipartite graphs)
2. Different Shapes: What happens if we use other shapes instead of circles, such as triangles or squares? Does the minimum number of colors change?
3. Single Line-Art Shape: Place a pencil on the paper and draw anything with a single line, distinct intersections, and so that the end and start are the same. How many colors are needed?