Introduction

In this activity, we'll explore patterns by finding the remainders when Fibonacci numbers are divided by other numbers.

Modulo

Sometimes, the most interesting part of dividing numbers is what's left over—the remainder. This is where the modulo(or mod) operator comes in. It gives us the remainder when one number is divided by another.

For example, when we divide 5 by 4, the remainder is 1.

This is written as 5 mod 4 = 1.

Here are a few to try:

• 6 mod 4 = ?
• 11 mod 2 = ?
• 2 mod 2 = ?

and then check:

Fibonacci

The Fibonacci sequence appears in a lot of math play and in nature. It is a sequence where each number is the sum of the two before it:

0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, ...

Start with 0 and 1. Each new number is the sum of the previous two numbers:

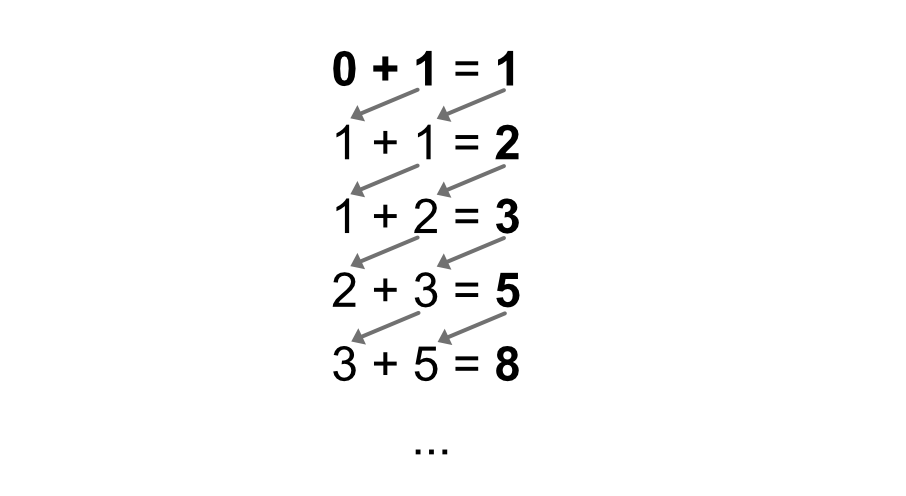
Here are the first few numbers of the sequence:

{0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 377, 610, 987, 1597, 2584, 4181, 6765, 10946, 17711, 28657, ...}

Here is a link to more numbers in the sequence.

Activity

• Use modular arithmetic with the Fibonacci sequence.
  • Try different ways to see what patterns emerge from finding the remainders.
• Form a conjecture(s) about what patterns are found.
  • Here is a tool for finding patterns.
• Test the conjecture with other numbers.

Activity Structure

This is a 45-60 minute activity exploring periodic patterns in number sequences.

Exploration Phase 1 (5-10 minutes)

Finding the First Patterns

Have learners explore the divisors 2 and 3, then come back with questions and ideas.

• Optional bridge: if you assign these patterns to notes - what do you hear?
  • Chrome music lab has a notes tool here.

Exploration Phase 2 - (10-15 minutes)

Once Patterns are Found

Introduce tools or tables to look at a couple more divisors (Example: start with 4,8, and 11). These larger numbers have longer sequences, and the goal isn't to be tedious, but to search for patterns. Allow for tools where they are helpful.

Here is a tool for finding patterns.

Here is a tool to listen to patterns and expand the soundscape- note that the periods are shown, so only use this if patterns have been found.

Also, here is a sound toy in Desmos with sound to play with as a facilitator (it is complex, but suitable for some situations).

Conjecture Formation (5-10 minutes)

Allow for time to write down observations and form conjectures. Give examples of conjectures if needed.

Example Conjectures:

Example: "The remainders repeat when the Fibonacci sequence is divided by a number."

Example: "The sequence follows Fibonacci rules: the previous two numbers add together to make the next number, but with modulo applied."

Example: "The length of each sequence relates to the modulus."

Supporting Questions:

• "What do these repeating sequences have in common?"
• "Is there a pattern to help you predict the next remainder?"
• "Are there families of divisors with similar patterns?"
• "Is there a pattern in the sequence lengths?"

If learners have a strong understanding of these periods, a table of the remainders may be helpful to form additional conjectures. Here is one for the first 100 divisors:

Discussion and Discovery (10-15 minutes)

• Share conjectures.
• Discuss different approaches.
• Use tools and investigate new questions as they come up.
• Guide learners toward different insights and introduce terminology.
  • Example: Looking beyond the divisors of 2 and 3, what other patterns are found?
    • The patterns that repeat are called Pisano Periods

Example Learner Conjectures

• "Fibonacci remainders always cycle back to the beginning."
• "The cycle length depends on what number you're dividing by."
• "You can tell when the cycle repeats by watching for 0,1 to appear again."

Optional - Proof

Example:

1. When dividing by n, remainders can only be 0, 1, 2, ..., n-1.
2. Each remainder depends on the previous pair of remainders.
3. There are only n² possible pairs of consecutive remainders.
4. In an infinite sequence, some pair must repeat (Pigeonhole Principle).
5. Once a pair repeats, the entire pattern repeats from that point.

Scaffolding understanding:

• Step 1: Understand the Remainders
  • To get the next remainder, add the two previous remainders, then take mod n.
    • Example: With mod 5, if we have 3, 4, then next is (3+4) mod 5 = 2.
    •  What's the next remainder after 2, 3 in mod 5?
      • (2+3) mod 5 = 0
• The rule always works the same way
  • If the pair (3, 4) appears anywhere in my sequence for mod 5, the next remainder is always 2.
• Step 2: Count the Possible Pairs
  • With mod n, remainders can only be 0, 1, 2, ..., n-1.
  • How many different pairs can we make?
    • n × n = n² pairs.
  • For mod 3: (0,0), (0,1), (0,2), (1,0), (1,1), (1,2), (2,0), (2,1), (2,2) = 9 pairs.
    • Check: How many pairs are possible with mod 4? [Answer: 16]
• Step 3: Pigeonhole Principle
  • If our sequence goes longer than n² pairs, we must see some pair twice
  • This is like having 9 boxes but 10 items - something goes in a box twice
    • Check: With mod 3, if our sequence has 10 consecutive pairs, what's guaranteed?
• Step 4: Tying it all together
  • When we see the same pair twice, everything after must repeat.
    • Why? Because identical pairs always produce identical next steps.
    • And those identical next steps create identical pairs again...
    • Check: Look at the Pisano period for any given divisor.
• Different ways to phrase a takeaway:
  • We run out of new pairs, so we have to repeat one - and that makes everything repeat.
  • There are only n² possible pairs, but infinitely many steps, so repetition is inevitable.

Tools and Supplies

• Fibonacci numbers or generator.
• Calculator or computer for Fibonacci sequence generation.
• Paper/spreadsheet for recording remainder sequences.
• Modular arithmetic tool/website (see tool in intro).

Vocabulary

• Conjecture: A mathematical statement that is believed to be true but has not yet been proven.
• Counterexample: A specific example that disproves a conjecture.
• Modular arithmetic: Mathematics of remainders.
• Pisano period: The length of the repeating cycle when Fibonacci numbers are taken modulo n.
• Cardinality: The number of elements in a set.
• Cycle/Period: A repeating pattern in a sequence.
• Remainder: What's left over after division.
• Modulo/Mod: The operation that finds the remainder when one number is divided by another.
• Deterministic: A process where the same inputs always produce the same outputs.
• Finite: Having a limited number of possibilities or elements.
• Sequence: An ordered list of numbers following a specific pattern or rule.
• State: In this context, a pair of consecutive remainders that determines what comes next.
• Pigeonhole Principle: If you have more items than containers, at least one container must hold more than one item.

Extensions and What Ifs

• Can any positive integer divide at least one Fibonacci number evenly?
• Historical note: These are called Pisano periods, named after Leonardo Pisano (Fibonacci).
• Pattern hunting: Pisano periods for primes, for powers of primes, for composite numbers.
  • Example: π(2) = 3, π(5) = 20, and π(10) = 60.
• Pisano periods of Fibonacci numbers
• Open questions: Is there a formula for Pisano periods?
• Other sequences: Do similar periodic patterns emerge with different starting sequences (Lucas numbers, Tribonacci)?