Inquiries-Week 6: Beautiful Chords

Introduction

In this inquiry, we explore chords, which are lines drawn across circles, using different rules to create various patterns, curves, and shapes. This inquiry will be different from those in the Inquiries Series in that it will be more open, with a focus on math + art play.

Activity 1: String Play

1. Draw a circle on paper, on a computer, on fabric, with nails on wood, or whatever medium you choose. Make this circle have evenly spaced points around it - you can choose how many you'd like.

Note: there are digital tools for this inquiry, but actual string on pinboards, fabric, wood, paper, and other materials is encouraged. Art is a process, and playing with materials adds to the experience of exploration.

2. Make some rules for connecting points on your circle:

Example: Skip 3 points between each connection:

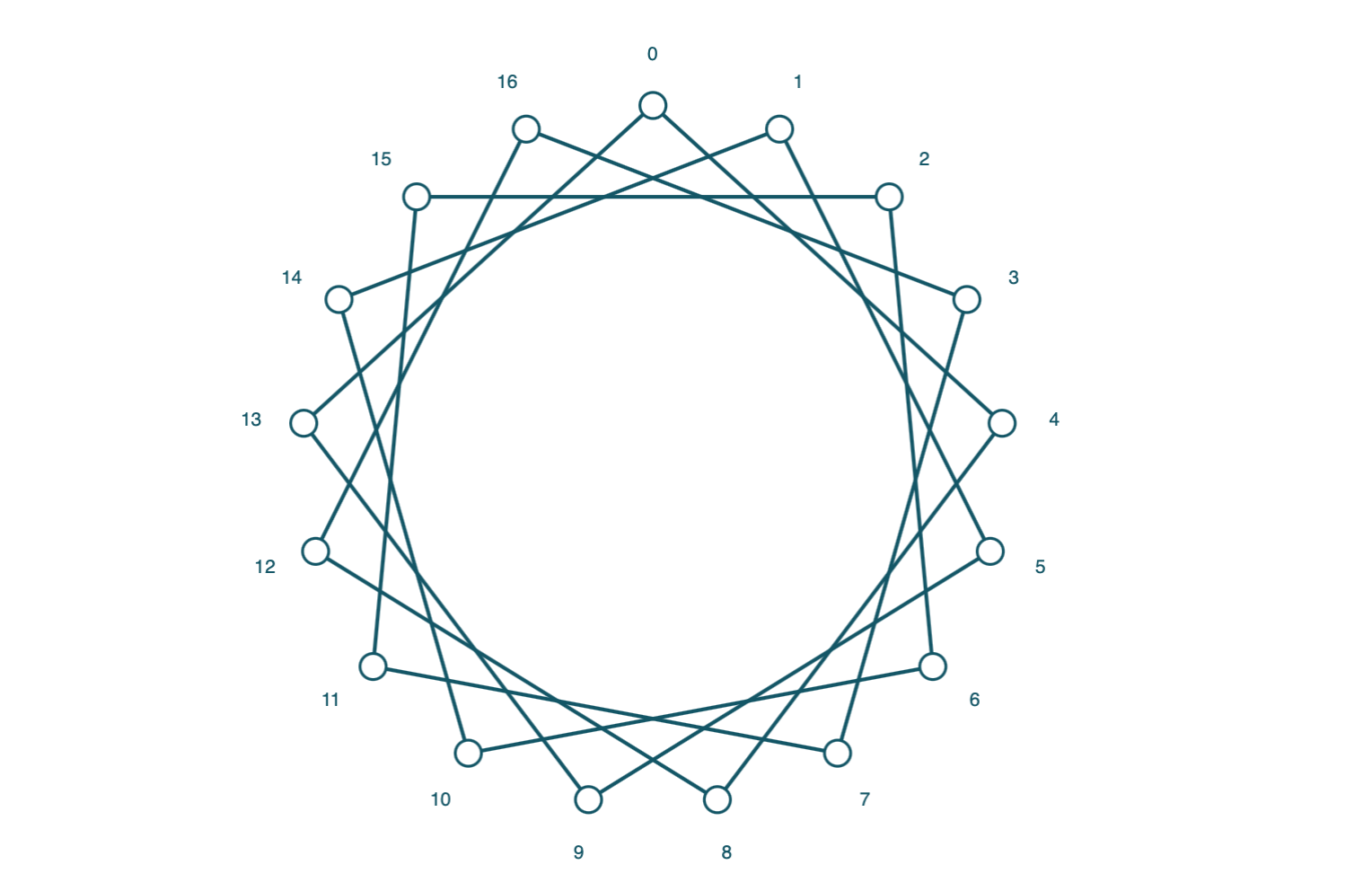
Example: Connect every point to every point:

3. Follow your rules to see what emerges. Here is a tool to do this on a computer, and also below:

4. Think about the what-ifs and ways to play:
   1. What questions do you have about your rules and patterns?
   2. What happens if you change something about your rules?
   3. Can you form a conjecture and test small changes to your rules?
   4. Do small changes in your rules make small or large changes in the patterns formed by chords?
   5. What other rules for connecting points are interesting to explore?

Activity 2: Thinking in steps

1. Below is a toy that has rules for drawing chords. Can you figure out what those rules are? (here is a full page version)
   1. What are Step A and Step B?

2. Once you find the rules, what patterns do you see using these rules?
   1. Think about the shapes, symmetries, subtle patterns, petals, how it is drawn, etc.
3. Gather data for the patterns that interest you in a central location.
4. Form conjectures about the patterns using the data.
5. Test those conjectures.

Activity 3: Thinking with multipliers

Perform the same inquiry as Activity 2, but this time with a different toy with different rules for drawing chords. (here is a full page version)

Formulate questions about your discoveries, form, and test conjectures.

Examples of other questions:

• How do these rules compare to the previous rules?
• Is there a way to apply a rule with a multiplier that equals the rules with the steps?
• Are there different or similar patterns?
• Are there patterns that happen with one set of rules and not another?
• Form and test conjectures.

Further Activities and explorations with chords?

• Instead of connecting one circle's points, what about connecting one shape to another - circles with circles, circles with ellipses, lines with lines, 3D shapes (here is a tool to play with two ellipses) - What if shapes are rotated with strings attached?

• Random chord play - how long are chords? What is the average length of random chords?

• How could you control the pattern or draw pictures with chords? Are there algorithms to explore or invent?
• What moire patterns emerge with different chord configurations and overlapping of shapes?
• What do Games of Life (cellular automata) look like with chords as connections (lots of neighbors)?