M
Sign in Subscribe

Filtering Snowflakes

Sophia Wood

• 2 min read
A hexagon with triangles of blues and peaches symmetrically placed throughout creating strong lines of diamons on the center to vertex lines. On a blue background.

Whether you call this triangle Pascal's triangle, Binomial Expansion Coefficients, Yang Hui's triangle, or any other name, it is beautiful.

Pascal's Triangle hand written in autumn orange lettering for the first 7 rows with three dots at the bottom.

Finding patterns in this triangle is fun - from counting numbers, to looking at parity (even/odd-ness), to primes and other numbers. When we look for certain numbers, we can think of it as filtering or sieving.

I played with different filters to overlay and then rotated copies of the triangles to make snowflakes. If you'd like to play, there is a very rough prototype here.

I made a few snowflakes using it:

On a light yellow background, a hexagon with blue and yellow and browns mixed with Sierpinski-like triangles arranged throughout.
on a pink background, light patterns, then darker triangle overlays all pointing to the edges of a hexagon with symmetry. the lines from the center to vertices are dotted with darker pinks and oranges.
A dark purple background with a hexagon showing faint patterns of sierpinsky triangles and other patterning with what feels like noise. the colors are dark pinks and light teals throughout.
light blue-green background with green triangle patterns in the hexagon throughout all pointing to the edges with symmetry. there is negative space on the lines going from the center to the vertices.
on a dark background a hexagon with symmetrical hexagon tiling with peaches and greens and browns making subtle smaller hexagons and stars within.

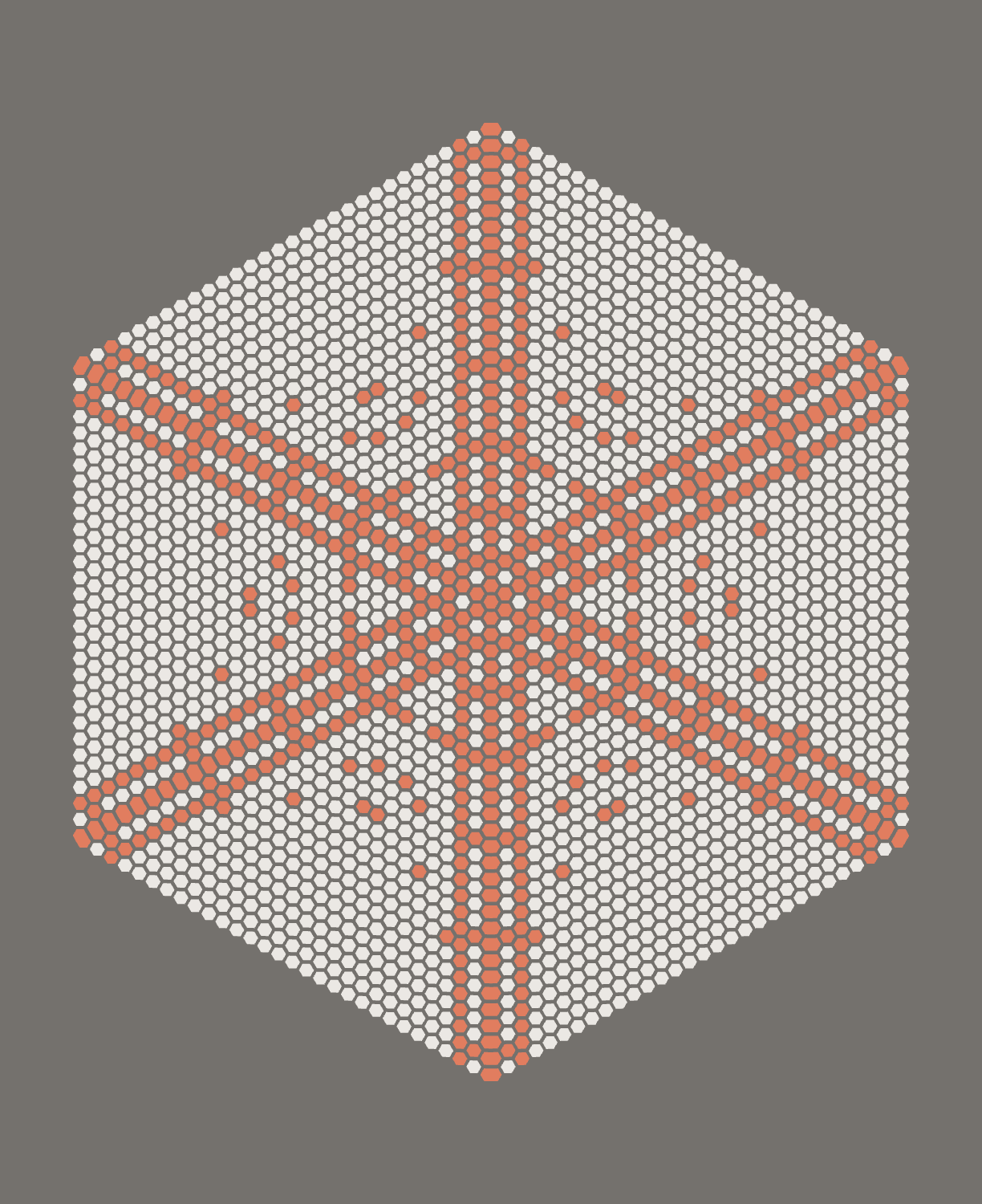
Some notes for inquiry:

  • Can you predict modular arithmetic patterns?
    • Example: look at mod 10 and compare it to mod 2 and mod 5
  • How do the odious-like (base-n parity) patterns compare to modular arithmetic?
  • Where are primes scarce? why?
  • Can you overlay filters to make equivalent filters?
  • What patterns are interesting when zoomed in? zoomed out? both?
  • Some numbers (such as Fibonacci numbers) were left out because they are less interesting at this scale. What are other numbers that might be like this?

Sign up for more like this.

Enter your email
Subscribe

Want to become a better programmer? Join the Recurse Center!

Sophia

Mathematics educator and creative coder exploring the beauty of mathematical concepts through interactive visualizations and playful learning.

Mathematics

Education

Creative Coding